Lũy thừa là một khái niệm quan trọng trong chương trình Toán THPT và thường xuyên xuất hiện trong các kỳ thi. Để giúp các bạn học sinh nắm vững kiến thức và giải quyết bài tập một cách hiệu quả, bài viết này sẽ tập trung vào một dạng toán đặc biệt: Cộng Lũy Thừa Cùng Cơ Số. Chúng ta sẽ cùng nhau khám phá định nghĩa, công thức và các bài tập vận dụng liên quan đến cộng lũy thừa cùng cơ số.
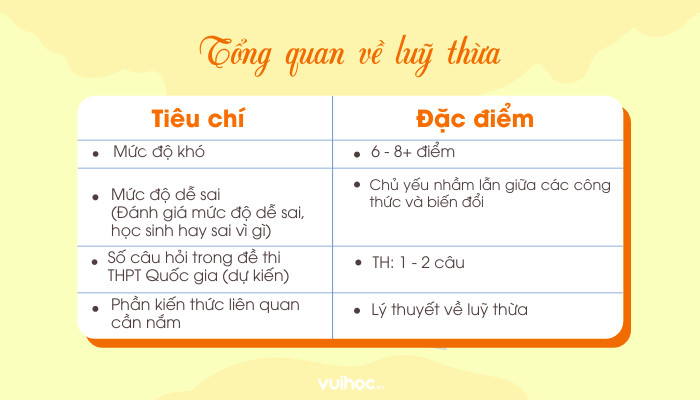
Tổng quan về kiến thức lũy thừa và cộng lũy thừa cùng cơ số, giúp học sinh dễ dàng hình dung độ khó trong các bài thi.
1. Ôn Lại Kiến Thức Nền Tảng Về Lũy Thừa
Trước khi đi sâu vào cộng lũy thừa cùng cơ số, chúng ta cần nắm vững những kiến thức cơ bản về lũy thừa.
1.1. Định Nghĩa Lũy Thừa
Lũy thừa là phép toán thực hiện trên hai số a và b, ký hiệu là $a^b$, đọc là “a mũ b” hoặc “lũy thừa bậc b của a”. Trong đó:
- a là cơ số.
- b là số mũ.
Lũy thừa $a^b$ được hiểu là tích của b thừa số a nhân với nhau:
$a^b = a a a … a$ (b thừa số a)
1.2. Các Dạng Lũy Thừa Thường Gặp
Trong chương trình THPT, chúng ta làm quen với ba dạng lũy thừa chính:
- Lũy thừa với số mũ nguyên: Số mũ là một số nguyên (ví dụ: $2^3, 5^{-2}$).
- Lũy thừa với số mũ hữu tỉ: Số mũ là một số hữu tỉ (ví dụ: $4^{frac{1}{2}}, 9^{frac{3}{2}}$).
- Lũy thừa với số mũ thực: Số mũ là một số thực (ví dụ: $3^{pi}, 7^{sqrt{2}}$).
1.3. Tính Chất Quan Trọng Của Lũy Thừa
Các tính chất của lũy thừa là công cụ không thể thiếu để biến đổi và rút gọn các biểu thức chứa lũy thừa, đặc biệt là trong các bài toán cộng lũy thừa cùng cơ số. Dưới đây là một số tính chất quan trọng:
- $a^m * a^n = a^{m+n}$ (Nhân hai lũy thừa cùng cơ số)
- $frac{a^m}{a^n} = a^{m-n}$ (Chia hai lũy thừa cùng cơ số)
- $(a^m)^n = a^{m*n}$ (Lũy thừa của lũy thừa)
- $(ab)^m = a^m b^m$
- $(frac{a}{b})^m = frac{a^m}{b^m}$
2. Khám Phá Cộng Lũy Thừa Cùng Cơ Số
2.1. Định Nghĩa
Cộng lũy thừa cùng cơ số là phép toán cộng các lũy thừa có cùng cơ số với nhau. Ví dụ: $2^3 + 2^5$, $3^2 + 3^4 + 3^6$.
2.2. Phương Pháp Giải Bài Toán Cộng Lũy Thừa Cùng Cơ Số
Không có công thức trực tiếp cho việc cộng lũy thừa cùng cơ số. Tuy nhiên, chúng ta có thể sử dụng các phương pháp sau để giải quyết các bài toán này:
- Đặt nhân tử chung: Nếu các số mũ có thể đưa về dạng chung (ví dụ: $a^n + a^{n+2} = a^n + a^n * a^2 = a^n(1+a^2)$), ta có thể đặt nhân tử chung để đơn giản hóa biểu thức.
- Sử dụng hằng đẳng thức: Trong một số trường hợp, biểu thức có thể được đưa về dạng hằng đẳng thức quen thuộc (ví dụ: $(a+b)^2, (a-b)^2, a^2 – b^2$).
- Tính trực tiếp: Nếu các số mũ nhỏ, ta có thể tính trực tiếp giá trị của từng lũy thừa rồi cộng lại.
2.3. Ví Dụ Minh Họa
Ví dụ 1: Tính giá trị của biểu thức $2^3 + 2^5$.
- Cách 1: Tính trực tiếp: $2^3 + 2^5 = 8 + 32 = 40$.
- Cách 2: Đặt nhân tử chung: $2^3 + 2^5 = 2^3 + 2^3 2^2 = 2^3(1 + 2^2) = 8 5 = 40$.
Ví dụ 2: Rút gọn biểu thức $3^2 + 3^4 + 3^6$.
- Đặt $t = 3^2$, ta có: $3^2 + 3^4 + 3^6 = t + t^2 + t^3 = t(1 + t + t^2) = 3^2(1 + 3^2 + (3^2)^2) = 9(1 + 9 + 81) = 9 * 91 = 819$.
Bảng tổng hợp các công thức lũy thừa cùng cơ số và khác cơ số thường gặp.
3. Bài Tập Vận Dụng
Để củng cố kiến thức về cộng lũy thừa cùng cơ số, hãy cùng nhau giải một số bài tập sau:
Bài 1: Tính giá trị của biểu thức $5^2 + 5^3 – 5^1$.
Bài 2: Rút gọn biểu thức $x^3 + x^5 + x^7$ (với x ≠ 0).
Bài 3: Cho $A = 7 + 7^2 + 7^3 + … + 7^{100}$. Chứng minh rằng $6A + 7$ là một lũy thừa của 7.
Hướng dẫn giải:
- Bài 1: $5^2 + 5^3 – 5^1 = 25 + 125 – 5 = 145$.
- Bài 2: $x^3 + x^5 + x^7 = x^3(1 + x^2 + x^4)$.
- Bài 3: $6A = 6(7 + 7^2 + 7^3 + … + 7^{100}) = 42 + 67^2 + 67^3 + … + 67^{100}$. Khi đó $6A + 7 = 49 + 67^2 + 67^3 + … + 67^{100}$. Cần biến đổi thêm để chứng minh biểu thức này là một lũy thừa của 7. (Gợi ý: Biến đổi 49 thành $7^2$ và nhóm các số hạng thích hợp).
4. Kết Luận
Cộng lũy thừa cùng cơ số là một dạng toán thường gặp trong chương trình Toán THPT. Để giải quyết các bài toán này, chúng ta cần nắm vững kiến thức về lũy thừa, các tính chất của lũy thừa và các phương pháp biến đổi biểu thức. Hy vọng bài viết này đã cung cấp cho các bạn những kiến thức và kỹ năng cần thiết để chinh phục các bài toán cộng lũy thừa cùng cơ số một cách hiệu quả. Chúc các bạn học tốt!