Trong hình học, việc chứng minh một tam giác là vuông trong đường tròn là một kỹ năng quan trọng. Dưới đây là các phương pháp và bài tập giúp bạn nắm vững kiến thức này, đặc biệt hữu ích cho kỳ thi tuyển sinh vào lớp 10.
Các Phương Pháp Chứng Minh Tam Giác Vuông
Để chứng minh một tam giác là vuông trong đường tròn, ta có thể sử dụng một trong các phương pháp sau:
- Định nghĩa: Chứng minh tam giác có một góc vuông.
- Định lý Pytago đảo: Nếu bình phương cạnh lớn nhất bằng tổng bình phương hai cạnh còn lại, tam giác đó là tam giác vuông.
- Định lý về góc nội tiếp chắn nửa đường tròn: Nếu một tam giác nội tiếp đường tròn và có một cạnh là đường kính của đường tròn, thì tam giác đó là tam giác vuông. Đây là một trong những cách phổ biến và hiệu quả nhất để chứng minh tam giác vuông trong đường tròn.
Cách dựng tam giác ABC vuông tại A khi biết cạnh huyền BC và cạnh góc vuông AC:
- Dựng đoạn AC.
- Dựng góc CAx bằng 90 độ.
- Dựng cung tròn tâm C bán kính BC cắt Ax tại B. Nối BC ta được tam giác ABC vuông tại A.
Bài Tập Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng các phương pháp trên, hãy cùng xem xét một số ví dụ cụ thể.
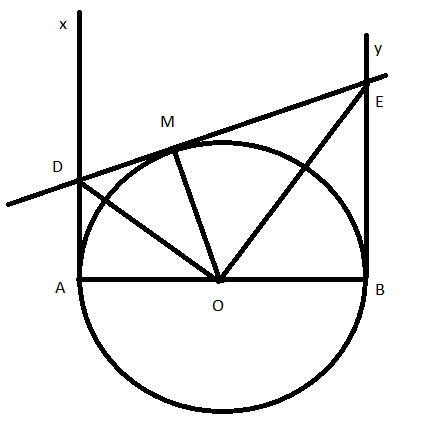
Bài 1: Cho nửa đường tròn (O) đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O). Tiếp tuyến thứ ba tiếp xúc với nửa đường tròn (O) tại M cắt Ax, By lần lượt tại D và E. Chứng minh tam giác DOE là tam giác vuông.
Lời giải:
Sơ đồ chứng minh tam giác DOE vuông tại O, sử dụng tính chất tiếp tuyến và góc kề bù
-
Có Ax và MD là hai tiếp tuyến cắt nhau tại D suy ra OD là tia phân giác của (widehat {AOM})
-
Có By và ME là hai tiếp tuyến cắt nhau tại E suy ra OE là tia phân giác của (widehat {BOM})
-
Có (widehat {AOM})và (widehat {BOM}) là hai góc kề bù suy ra (widehat {BOM} + widehat {AOM} = {90^0})
Mà (widehat {AOD} = widehat {DOM} = frac{{widehat {AOM}}}{2})(OD là tia phân giác của (widehat {AOM}))
Và (widehat {BOE} = widehat {MOE} = frac{{widehat {BOM}}}{2})(OE là tia phân giác của (widehat {BOM}))
Suy ra ta có
(begin{array}{l} 2widehat {DOM} + 2widehat {MOE} = {180^0}\ Leftrightarrow widehat {DOM} + widehat {MOE} = {90^0}\ Leftrightarrow widehat {DOE} = {90^0} end{array})
Vậy tam giác DOE là tam giác vuông.
Bài 2: Cho tam giác ABC vuông ở A. Dựng ở miền ngoài tam giác ABC các hình vuông ABHK, ACD. Đường thẳng HD cắt đường tròn ngoại tiếp tam giác ABC tại F, chứng minh FBC là tam giác vuông cân.
Hướng dẫn giải:
Ta có (widehat{BFC} = 90^{0}) (nội tiếp chắn nửa đường tròn) nên tam giác BFC vuông tại F. (1).
(widehat{FBC} = widehat{FAC}) (nội tiếp cùng chắn cung FC) mà theo trên (widehat{CAD} = 45^{0}) hay (widehat{FAC} = 45^{0}) (2).
Từ (1) và (2) suy ra ∆FBC là tam giác vuông cân tại F.
Bài 3: Cho đường tròn (O), BC là dây bất kì (BC
Minh họa bài toán chứng minh tam giác cân và tính chất nội tiếp trong đường tròn
Bài Tập Tự Luyện
Để củng cố kiến thức và rèn luyện kỹ năng, bạn có thể thử sức với các bài tập sau:
Bài 1: Cho đường tròn (O; R) đường kính AB. M là trung điểm của OA. Kẻ dây CD vuông góc với OA tại M. Chứng minh tam giác BCD đều.
Bài 2: Cho đường tròn (O; R), M là một điểm ở ngoài đường tròn sao cho OM = 2R. Tia MO cắt đường tròn ở A và B (A nằm giữa M và O). Từ M kẻ 2 tiếp tuyến MC và MD với đường tròn (O), H là giao điểm của MO với CD. Chứng minh tam giác MCD là tam giác đều.
Bài 3: Từ một điểm ở ngoài đường tròn (O), kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Gọi I là trung điểm của đoạn AB, kẻ tiếp tuyến IM với đường tròn (O) (M là tiếp điểm). Chứng minh tam giác ABM là tam giác vuông.
Bài 4: Cho đường tròn tâm O. Gọi I là trung điểm của bán kính OA. Qua I kẻ dây BC vuông góc với OA. Chứng minh tứ giác ABOC là hình thoi
Bài 5: Cho đường tròn tâm O bán kính R, đường kính AB. M là trung điểm của AO. Kẻ dây CD vuông góc với OA tại M. Chứng minh tam giác BCD đều
Nắm vững các phương pháp chứng minh và luyện tập thường xuyên với các bài tập, bạn sẽ tự tin giải quyết các bài toán liên quan đến tam giác vuông trong đường tròn. Chúc bạn thành công trong kỳ thi sắp tới!