Nguyên hàm là một khái niệm then chốt trong giải tích, và việc nắm vững các công thức, đặc biệt là nguyên hàm của các hàm số đơn giản, là vô cùng quan trọng. Bài viết này sẽ đi sâu vào công thức nguyên hàm của hàm số dạng 1/(ax+b), cùng các ví dụ minh họa và bài tập áp dụng để bạn đọc dễ dàng nắm bắt và vận dụng.
Công Thức Tổng Quát
Nguyên hàm của hàm số 1/(ax+b) được tính theo công thức sau:
∫ (1/(ax+b)) dx = (1/a) * ln|ax+b| + C
Trong đó:
- a và b là các hằng số, với a ≠ 0.
- ln là logarit tự nhiên.
- C là hằng số tích phân.
Tại Sao Lại Có Công Thức Này?
Công thức này xuất phát từ quy tắc đạo hàm của hàm logarit. Ta biết rằng đạo hàm của ln|x| là 1/x. Áp dụng quy tắc chuỗi (chain rule) cho hàm ln|ax+b|, ta có:
d/dx (ln|ax+b|) = (1/(ax+b)) * a
Do đó, để tìm nguyên hàm của 1/(ax+b), ta cần triệt tiêu hệ số a bằng cách chia cho a, dẫn đến công thức (1/a) * ln|ax+b| + C.
Ví Dụ Minh Họa
Để hiểu rõ hơn, chúng ta sẽ xét một số ví dụ cụ thể:
Ví dụ 1: Tìm nguyên hàm của 1/(2x+3).
Áp dụng công thức, ta có:
∫ (1/(2x+3)) dx = (1/2) * ln|2x+3| + C
Ví dụ 2: Tìm nguyên hàm của 1/(x-1).
Ở đây, a = 1 và b = -1, nên:
∫ (1/(x-1)) dx = (1/1) * ln|x-1| + C = ln|x-1| + C
Ví dụ 3: Tìm nguyên hàm của 1/(-3x+5).
Trong trường hợp này, a = -3 và b = 5, vậy:
∫ (1/(-3x+5)) dx = (1/-3) ln|-3x+5| + C = – (1/3) ln|-3x+5| + C
Các Trường Hợp Đặc Biệt
Nếu a = 1, công thức trở thành:
∫ (1/(x+b)) dx = ln|x+b| + C
Đây là một trường hợp thường gặp và dễ nhớ.
Bài Tập Áp Dụng
Để củng cố kiến thức, hãy thử giải các bài tập sau:
- Tìm nguyên hàm của 1/(4x+1).
- Tìm nguyên hàm của 1/(2-x).
- Tìm nguyên hàm của 1/(5x-3).
- Tìm nguyên hàm của 1/(-x+7).
- Tìm nguyên hàm của 1/(x+2).
Gợi ý: Áp dụng công thức (1/a) * ln|ax+b| + C cho mỗi bài tập, xác định đúng giá trị của a và b.
Ứng Dụng Thực Tế
Công thức nguyên hàm của 1/(ax+b) không chỉ là một kiến thức toán học thuần túy mà còn có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như:
- Vật lý: Tính toán liên quan đến sự thay đổi theo thời gian của các đại lượng vật lý.
- Kinh tế: Mô hình hóa tốc độ tăng trưởng hoặc suy giảm.
- Xác suất thống kê: Tính toán các hàm mật độ xác suất.
Mở Rộng Kiến Thức
Để nâng cao khả năng giải toán, bạn nên làm quen với các phương pháp tìm nguyên hàm khác như:
- Phương pháp đổi biến số: Sử dụng phép thay thế để đơn giản hóa biểu thức.
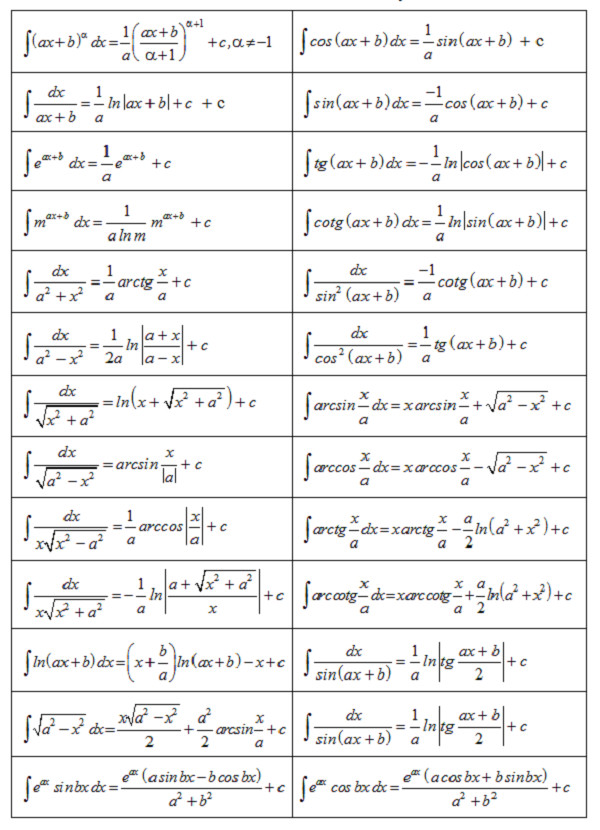
Alt: Bảng tổng hợp các công thức nguyên hàm mở rộng thường dùng trong giải tích, giúp học sinh dễ dàng tra cứu và áp dụng.
- Phương pháp tích phân từng phần: Áp dụng khi biểu thức tích phân có dạng tích của hai hàm số.
Alt: Tổng hợp các dạng bài tập nguyên hàm từng phần phổ biến, giúp học sinh nhận diện và áp dụng phương pháp giải phù hợp.
- Sử dụng bảng công thức nguyên hàm: Tra cứu bảng công thức để tìm nguyên hàm của các hàm số phức tạp hơn.
Alt: Bảng công thức nguyên hàm nâng cao, bao gồm các hàm số lượng giác, mũ, và logarit phức tạp, hỗ trợ giải các bài toán khó.
Kết Luận
Hiểu rõ và vận dụng thành thạo công thức nguyên hàm của 1/(ax+b) là một bước quan trọng để chinh phục môn giải tích. Hãy luyện tập thường xuyên và kết hợp với các phương pháp khác để nâng cao kỹ năng giải toán của bạn. Chúc bạn thành công!