Góc giữa đường thẳng và mặt phẳng là một khái niệm quan trọng trong hình học không gian lớp 11. Việc nắm vững lý thuyết và phương pháp xác định góc này sẽ giúp học sinh giải quyết các bài toán liên quan một cách hiệu quả. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách xác định góc giữa đường thẳng và mặt phẳng, từ cơ bản đến nâng cao, kèm theo các ví dụ minh họa và bài tập trắc nghiệm.
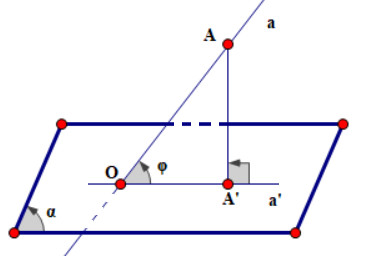
1. Định Nghĩa và Ký Hiệu Góc Giữa Đường Thẳng và Mặt Phẳng
1.1. Định Nghĩa
- Trường hợp 1: Nếu đường thẳng vuông góc với mặt phẳng, góc giữa chúng bằng 90°.
- Trường hợp 2: Nếu đường thẳng không vuông góc với mặt phẳng, góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó được gọi là góc giữa đường thẳng và mặt phẳng.
, đây là ký hiệu toán học thể hiện đường thẳng vuông góc với mặt phẳng.
Hình ảnh minh họa cách xác định góc giữa đường thẳng và mặt phẳng, trong đó góc α là góc cần tìm.
1.2. Ký Hiệu
- Nếu α ⊥ (P) thì góc giữa α và (P) bằng 90°. Ký hiệu: }=90^{0}).
- Nếu α không vuông góc với (P), góc giữa α và (P) là góc giữa α và α’, với α’ là hình chiếu của α trên (P). Ký hiệu:
Lưu ý quan trọng: 0° ≤ (góc giữa đường thẳng và mặt phẳng) ≤ 90°. Ký hiệu: .
2. Các Phương Pháp Xác Định Góc Giữa Đường Thẳng và Mặt Phẳng
2.1. Phương Pháp Vectơ
Phương pháp này sử dụng tích vô hướng của vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
- Gọi u là vectơ chỉ phương của đường thẳng d.
- Gọi n là vectơ pháp tuyến của mặt phẳng (P).
Khi đó, góc α giữa đường thẳng d và mặt phẳng (P) được tính theo công thức:
%7D)%20=%20%5Cfrac%7B%7C%5Cvec%7Bu%7D.%5Cvec%7Bn%7D%7C%7D%7B%7C%5Cvec%7Bu%7D%7C.%7C%5Cvec%7Bn%7D%7C%7D%20=%20%5Cfrac%7B%7Ca.A%20+%20b.B%7C%7D%7B%5Csqrt%7Ba%5E%7B2%7D%7D+b%5E%7B2%7D%5Csqrt%7BA%5E%7B2%7D+B%5E%7B2%7D%7D%7D)
Ví dụ: Cho tứ diện ABCD có AB, BC, BD đôi một vuông góc và bằng nhau. Xác định góc giữa AC và mặt phẳng (BCD).
Giải:
Hình ảnh minh họa tứ diện ABCD để xác định góc giữa AC và mặt phẳng (BCD).
Từ giả thiết, ta có: AB ⊥ BC. Suy ra AB ⊥ (BCD). Do đó, góc giữa AC và (BCD) là góc ACB.
2.2. Phương Pháp Hình Học
Đây là phương pháp thường được sử dụng để xác định góc giữa đường thẳng và mặt phẳng trong không gian.
- Bước 1: Tìm giao điểm I của đường thẳng d và mặt phẳng (P).
- Bước 2: Từ một điểm A thuộc d (A khác I), kẻ AH vuông góc với (P) tại H.
- Bước 3: Góc giữa đường thẳng d và mặt phẳng (P) là góc AIH.
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của BC. Biết tam giác SBC là tam giác đều. Tính góc giữa SA và (ABC).
Giải:
Hình ảnh minh họa hình chóp S.ABC để xác định góc giữa SA và mặt phẳng (ABC).
Vì H là hình chiếu của S lên (ABC) nên SH ⊥ (ABC). Vậy AH là hình chiếu của SA lên (ABC). Do đó, góc giữa SA và (ABC) là góc SAH. Vì SH ⊥ AH và tam giác ABC = tam giác SBC nên SH = AH. Tam giác SAH vuông cân tại H, suy ra góc SAH = 45°.
3. Bài Tập Trắc Nghiệm Về Góc Giữa Đường Thẳng và Mặt Phẳng
Câu 1: Cho hình thoi ABCD tâm O, AC = 2a, BD = 2AC. Lấy điểm S không thuộc (ABCD) sao cho SO ⊥ (ABCD). Biết tan(SBO) = 1/2. Tính góc giữa SC và (ABCD).
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính góc giữa SA và (ABC).
Câu 3: Cho hình chóp S.ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Tính góc giữa SC và (BHK).
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Tính góc giữa BD và (SAD).
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = a√6. Tính góc giữa SC và (ABCD).
Câu 6: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính góc giữa AC và (A’BCD’).
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 2a và SA vuông góc với mặt phẳng đáy (ABCD). Tính góc giữa cạnh SC và mặt phẳng (ABCD).
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, cạnh bên SA vuông góc với đáy. Góc giữa SC và đáy ABCD bằng 60°. Tính độ dài SA.
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B, AB = BC = a, AD = 2a, SA vuông góc với mặt phẳng đáy (ABCD). Tính độ dài SA để góc giữa SC và mặt phẳng (ABCD) bằng 45°.
Câu 10: Cho hình chóp S.ABC có SA = a, SA vuông góc với đáy, ABC là tam giác vuông cân tại B, góc ACB = 30°, AC = 2a. Tính tan(α) góc giữa SC và mặt phẳng (SAB).
Hy vọng qua bài viết này, các em học sinh sẽ nắm vững cách xác định góc giữa đường thẳng và mặt phẳng, từ đó giải quyết các bài toán hình học không gian một cách dễ dàng và chính xác.