Đường hypebol là một trong những đường conic quan trọng trong toán học, xuất hiện nhiều trong cả lý thuyết và ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về đường Hypebol, bao gồm định nghĩa, phương trình chính tắc, các tính chất hình học quan trọng và các bài tập áp dụng.
1. Định Nghĩa Đường Hypebol
Đường hypebol là tập hợp tất cả các điểm trên mặt phẳng sao cho giá trị tuyệt đối của hiệu khoảng cách từ mỗi điểm đó đến hai điểm cố định (gọi là tiêu điểm) là một hằng số. Hằng số này thường được ký hiệu là 2a, trong đó ‘a’ là độ dài bán trục thực của hypebol.
Hai điểm cố định được gọi là tiêu điểm, ký hiệu là F1 và F2. Đường thẳng đi qua hai tiêu điểm là trục thực của hypebol, và trung điểm của đoạn thẳng F1F2 là tâm của hypebol.
Định nghĩa bằng ký hiệu:
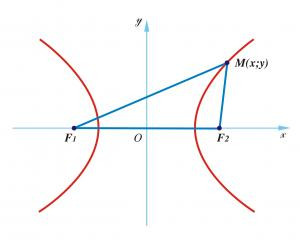
Cho hai điểm cố định F1, F2 với F1F2 = 2c (c > 0) và hằng số a. Đường hypebol (H) là tập hợp các điểm M thỏa mãn:
|MF1 – MF2| = 2a
Trong đó:
- F1 và F2 là tiêu điểm của đường hypebol (H).
- Khoảng cách F1F2 = 2c là tiêu cự của (H).
Hình ảnh minh họa định nghĩa đường hypebol, chú thích rõ các thành phần tiêu điểm (F1, F2), điểm M trên hypebol và các khoảng cách liên quan.
2. Phương Trình Chính Tắc của Đường Hypebol
2.1. Phương Trình
Trong hệ tọa độ Oxy, nếu đặt tiêu điểm F1(-c; 0) và F2(c; 0), phương trình chính tắc của đường hypebol có dạng:
x²/a² – y²/b² = 1
Trong đó:
- b² = c² – a²
- a là bán trục thực.
- b là bán trục ảo.
- c là nửa tiêu cự.
Phương trình này thể hiện mối quan hệ giữa tọa độ (x, y) của mọi điểm nằm trên đường hypebol.
Hình ảnh minh họa phương trình chính tắc của đường hypebol, thể hiện rõ các bán trục a, b và hình chữ nhật cơ sở.
2.2. Ví Dụ
Ví dụ 1: Lập phương trình chính tắc của hypebol (H) biết trục thực và trục ảo lần lượt là 10 và 6.
Giải:
- Độ dài trục thực 2a = 10 => a = 5
- Độ dài trục ảo 2b = 6 => b = 3
Phương trình chính tắc của hypebol là: x²/5² – y²/3² = 1 hay x²/25 – y²/9 = 1
Ví dụ 2: Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm cận là y = -3x.
Giải:
- Phương trình chính tắc: x²/a² – y²/b² = 1
- Đỉnh A2(5; 0) => a = 5
- Đường tiệm cận y = -3x => b/a = 3 => b = 3a = 15
Vậy phương trình chính tắc là: x²/5² – y²/15² = 1 hay x²/25 – y²/225 = 1
3. Hình Dạng và Tính Chất của Đường Hypebol
Đường hypebol có những đặc điểm và tính chất quan trọng sau:
-
Tiêu điểm: Hai tiêu điểm F1(-c; 0) và F2(c; 0).
-
Đỉnh: Hai đỉnh A1(-a; 0) và A2(a; 0).
-
Trục: Trục Ox là trục thực, trục Oy là trục ảo. Độ dài trục thực là 2a, trục ảo là 2b.
-
Nhánh: Đường hypebol gồm hai nhánh nằm hai bên trục ảo.
-
Hình chữ nhật cơ sở: Hình chữ nhật tạo bởi các đường thẳng x = ±a và y = ±b.
-
Đường tiệm cận: Hai đường thẳng chứa hai đường chéo của hình chữ nhật cơ sở, có phương trình y = ±(b/a)x.
-
Tâm sai: e = c/a > 1.
-
Khoảng cách từ điểm M(xM; yM) thuộc (H) đến tiêu điểm:
- MF1 = |a + exM| = |a + (c/a)xM|
- MF2 = |a – exM| = |a – (c/a)xM|
Ví dụ 1: Tìm tọa độ tiêu điểm, đỉnh, độ dài trục và phương trình tiệm cận của hypebol: x²/9 – y²/4 = 1
Giải:
- a = 3, b = 2, c = √(a² + b²) = √13
- Tiêu điểm: F1(-√13; 0), F2(√13; 0)
- Đỉnh: A1(-3; 0), A2(3; 0)
- Độ dài trục thực: 2a = 6, trục ảo: 2b = 4
- Tiệm cận: y = ±(2/3)x
Ví dụ 2: Cho hypebol (H) như hình dưới đây:
Hình ảnh minh họa bài tập về đường hypebol, yêu cầu chứng minh tính chất và xác định phương trình đường thẳng liên quan.
a) Chứng minh rằng nếu M(x, y) nằm trên (H) thì x ≤ -a hoặc x ≥ a.
b) Phương trình hai đường thẳng PR và QS có dạng như thế nào?
Giải:
a) M(x, y) thuộc (H) => x²/a² – y²/b² = 1. Vì y²/b² ≥ 0 => x²/a² ≥ 1 => x² ≥ a² => x ≤ -a hoặc x ≥ a.
b) P(-a, b), R(a; -b) => Vecto PR = (2a; -2b). Chọn vecto pháp tuyến n(b; a). Phương trình PR: b(x + a) + a(y – b) = 0 hay bx + ay = 0 hay y = -(b/a)x. Tương tự, phương trình QS: y = (b/a)x.
4. Bài Tập Áp Dụng
Dưới đây là một số bài tập trắc nghiệm về đường hypebol:
(Câu 1-20): (Nội dung và đáp án như trong bài viết gốc)
Các bài tập này giúp củng cố kiến thức về định nghĩa, phương trình, tính chất và các yếu tố liên quan đến đường hypebol.
Hy vọng bài viết này cung cấp cho bạn một cái nhìn tổng quan và chi tiết về đường hypebol, từ định nghĩa cơ bản đến các ứng dụng và bài tập thực hành. Việc nắm vững kiến thức về đường hypebol sẽ giúp ích rất nhiều trong quá trình học tập và nghiên cứu toán học.