Tam giác vuông là một hình học cơ bản nhưng vô cùng quan trọng, xuất hiện rộng rãi trong toán học, kỹ thuật, và đời sống hàng ngày. Bài viết này sẽ đi sâu vào Tính Chất Của Tam Giác Vuông, từ những định nghĩa cơ bản đến các ứng dụng thực tế, giúp bạn hiểu rõ hơn về hình học đặc biệt này.
Định Nghĩa và Các Yếu Tố Cơ Bản Của Tam Giác Vuông
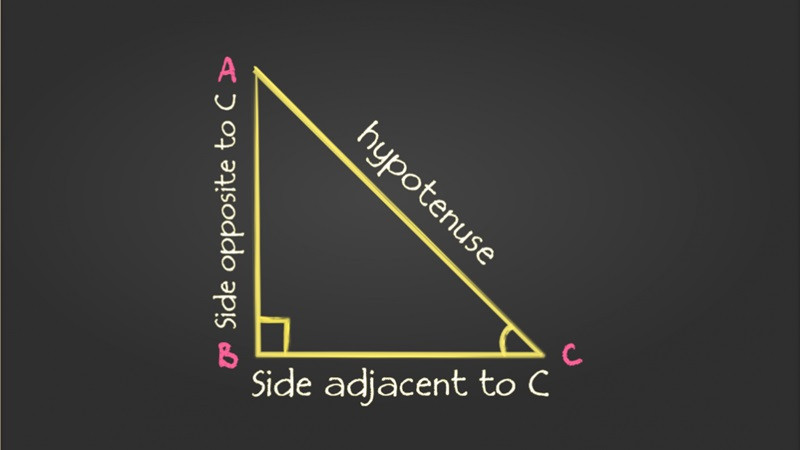
Tam giác vuông là tam giác có một góc vuông (90 độ). Cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại là cạnh góc vuông. Các tính chất của tam giác vuông giúp chúng ta giải quyết nhiều bài toán và ứng dụng trong thực tế.
Hình ảnh minh họa một tam giác vuông với các cạnh góc vuông và cạnh huyền được chú thích rõ ràng, cùng góc vuông 90 độ, giúp người đọc dễ dàng hình dung và nắm bắt khái niệm cơ bản.
Các yếu tố cơ bản của tam giác vuông:
- Góc vuông: Góc có số đo 90 độ.
- Cạnh huyền: Cạnh đối diện với góc vuông, là cạnh lớn nhất của tam giác vuông.
- Cạnh góc vuông: Hai cạnh tạo thành góc vuông.
Các Tính Chất Quan Trọng Của Tam Giác Vuông
Tam giác vuông sở hữu nhiều tính chất đặc biệt, là nền tảng cho nhiều công thức và ứng dụng trong toán học và các lĩnh vực khác.
-
Định lý Pythagoras: Đây là tính chất của tam giác vuông nổi tiếng nhất. Định lý phát biểu rằng: “Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Công thức:
a² + b² = c²(trong đó c là cạnh huyền, a và b là hai cạnh góc vuông).Hình ảnh trực quan về định lý Pythagoras, thể hiện mối quan hệ giữa các cạnh của tam giác vuông thông qua diện tích các hình vuông dựng trên mỗi cạnh.
-
Tổng hai góc nhọn: Trong một tam giác vuông, tổng hai góc nhọn (hai góc không phải góc vuông) luôn bằng 90 độ. Điều này xuất phát từ định lý tổng ba góc trong một tam giác bằng 180 độ.
-
Đường trung tuyến ứng với cạnh huyền: Đường trung tuyến ứng với cạnh huyền của tam giác vuông bằng một nửa cạnh huyền.
-
Các hệ thức lượng trong tam giác vuông: Các hệ thức lượng giác (sin, cos, tan, cot) có mối liên hệ chặt chẽ với các cạnh và góc của tam giác vuông.
Công Thức Tính Diện Tích và Đường Cao Trong Tam Giác Vuông
Diện tích tam giác vuông: Diện tích tam giác vuông bằng một nửa tích hai cạnh góc vuông.
Công thức: S = (1/2) * a * b (trong đó S là diện tích, a và b là hai cạnh góc vuông).
Đường cao trong tam giác vuông:
Hình ảnh thể hiện các đường cao, cạnh góc vuông và cạnh huyền của tam giác vuông, giúp người đọc hình dung và ghi nhớ công thức tính toán liên quan.
Có nhiều cách để tính đường cao trong tam giác vuông, tùy thuộc vào thông tin đã biết:
- Nếu biết diện tích và cạnh huyền:
h = (2 * S) / c(trong đó h là đường cao, S là diện tích, c là cạnh huyền). - Sử dụng hệ thức lượng: Ví dụ,
1/h² = 1/a² + 1/b²(trong đó h là đường cao, a và b là hai cạnh góc vuông).
Ứng Dụng Thực Tế Của Tam Giác Vuông
Tính chất của tam giác vuông không chỉ là kiến thức lý thuyết, mà còn có rất nhiều ứng dụng quan trọng trong thực tế:
-
Xây dựng và kiến trúc: Tam giác vuông được sử dụng để đảm bảo tính chính xác của các góc vuông trong công trình, tính toán diện tích và chiều cao, thiết kế các cấu trúc chịu lực.
Hình ảnh minh họa việc sử dụng tam giác vuông trong thiết kế và xây dựng các công trình, ví dụ như đo đạc góc vuông, đảm bảo tính chính xác của các cấu trúc.
-
Kỹ thuật: Tam giác vuông được ứng dụng trong thiết kế máy móc, tính toán lực và momen, phân tích kết cấu.
Hình ảnh minh họa việc sử dụng tam giác vuông trong thiết kế và phân tích các bộ phận máy móc, đảm bảo độ chính xác và hiệu quả hoạt động.
-
Đo đạc và định vị: Tam giác vuông được sử dụng trong các thiết bị đo đạc, giúp xác định khoảng cách và độ cao một cách chính xác.
-
Vật lý và cơ học: Tam giác vuông được sử dụng để phân tích lực, vận tốc, gia tốc, và các đại lượng vật lý khác.
Ví Dụ Minh Họa
Xét tam giác vuông ABC vuông tại A, có AB = 3cm, AC = 4cm.
- Tính cạnh huyền BC: Áp dụng định lý Pythagoras:
BC² = AB² + AC² = 3² + 4² = 25. Vậy BC = 5cm. - Tính diện tích tam giác ABC:
S = (1/2) * AB * AC = (1/2) * 3 * 4 = 6 cm².
Hình ảnh minh họa một bài toán cụ thể về tam giác vuông, với các cạnh và góc được cho trước, yêu cầu tính toán các yếu tố còn lại như cạnh huyền, diện tích, đường cao.
Kết Luận
Nắm vững các tính chất của tam giác vuông là nền tảng quan trọng trong toán học và các ứng dụng thực tế. Từ định lý Pythagoras đến các công thức tính diện tích và đường cao, kiến thức về tam giác vuông giúp chúng ta giải quyết nhiều vấn đề trong cuộc sống và công việc một cách hiệu quả. Hãy luyện tập thường xuyên để ghi nhớ và áp dụng thành thạo những kiến thức này!