Hình lục giác, đặc biệt là lục giác đều, là một hình học phổ biến trong cả toán học và đời sống. Bài viết này sẽ đi sâu vào khái niệm Chu Vi Lục Giác đều, cung cấp công thức tính, ứng dụng thực tế và các bài tập tự luyện, giúp bạn nắm vững kiến thức này một cách toàn diện.
Hình Lục Giác và Lục Giác Đều: Khái Niệm và Đặc Điểm
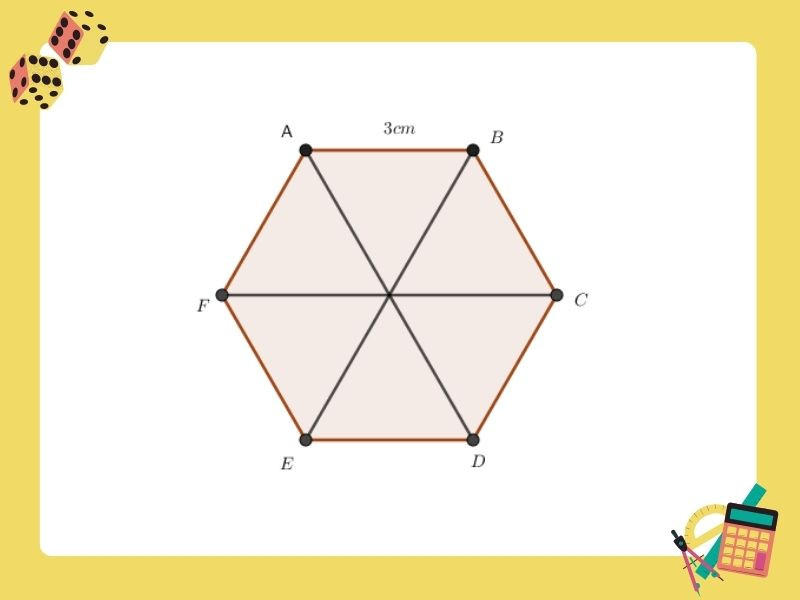
Hình lục giác là một đa giác có sáu cạnh và sáu góc. Điểm đặc biệt của hình lục giác đều là tất cả các cạnh và góc đều bằng nhau. Điều này tạo nên tính đối xứng và cân bằng, khiến hình lục giác đều xuất hiện nhiều trong tự nhiên và các ứng dụng kỹ thuật.
-
Đặc điểm của hình lục giác:
- 6 cạnh, 6 góc.
- Tổng số đo các góc trong một hình lục giác bất kỳ là 720 độ.
- Trong hình lục giác đều, mỗi góc có số đo là 120 độ.
-
Ứng dụng: Tổ ong, cấu trúc tinh thể, thiết kế ốc vít, gạch lát sàn, và nhiều ứng dụng khác.
Công Thức Tính Chu Vi Lục Giác Đều
Công thức tính chu vi lục giác đều rất đơn giản và dễ nhớ:
*Chu vi (P) = 6 a**
Trong đó:
- P: Chu vi của hình lục giác đều.
- a: Độ dài của một cạnh hình lục giác đều.
Lưu ý: Đối với hình lục giác không đều, bạn cần cộng độ dài của tất cả sáu cạnh để tính chu vi.
Ứng Dụng Thực Tế Của Chu Vi Lục Giác Đều
Công thức tính chu vi lục giác đều không chỉ là kiến thức toán học khô khan, mà còn có nhiều ứng dụng thiết thực trong cuộc sống:
- Kiến trúc và xây dựng: Tính toán vật liệu cần thiết cho các công trình có yếu tố lục giác, như gạch lát hình lục giác, mái vòm lục giác, v.v. Việc tính toán chính xác chu vi giúp tối ưu hóa vật liệu và đảm bảo tính thẩm mỹ.
- Thiết kế: Ứng dụng trong thiết kế các sản phẩm có hình dạng lục giác, ví dụ như hộp đựng, đồ trang trí, v.v.
- Sản xuất: Trong sản xuất các chi tiết máy móc có hình dạng lục giác, việc tính toán chu vi giúp đảm bảo kích thước chính xác.
- Tổ ong: Nghiên cứu cấu trúc tổ ong, một ví dụ điển hình về hình lục giác đều trong tự nhiên, để ứng dụng vào các thiết kế kỹ thuật.
Bài Tập Tự Luyện về Chu Vi Lục Giác Đều
Để củng cố kiến thức, bạn có thể tự luyện với các bài tập sau:
Bài 1: Một hình lục giác đều có cạnh dài 5cm. Tính chu vi của hình lục giác đó.
Bài 2: Một sân chơi trẻ em có hình lục giác đều, mỗi cạnh dài 8m. Người ta muốn làm hàng rào xung quanh sân chơi. Tính chiều dài hàng rào cần làm.
Bài 3: Một viên gạch lát nền hình lục giác đều có cạnh dài 30cm. Tính chu vi của viên gạch đó.
Bài 4: Một chiếc bàn trà có mặt bàn hình lục giác đều, chu vi mặt bàn là 360cm. Tính độ dài mỗi cạnh của mặt bàn.
Bài 5: Tìm chu vi của một hình lục giác đều nội tiếp trong một đường tròn có bán kính 4cm. (Gợi ý: Cạnh của lục giác đều bằng bán kính đường tròn ngoại tiếp).
Mở Rộng Tư Duy: Lục Giác Đều và Các Hình Học Khác
Hiểu rõ về chu vi lục giác đều mở ra cơ hội khám phá các mối liên hệ giữa lục giác đều và các hình học khác:
- Tam giác đều: Lục giác đều có thể được chia thành 6 tam giác đều bằng nhau.
- Hình vuông: Có thể tạo ra các họa tiết và cấu trúc phức tạp bằng cách kết hợp lục giác đều và hình vuông.
- Đường tròn: Lục giác đều có thể nội tiếp trong một đường tròn và ngược lại.
Nắm vững công thức tính chu vi lục giác đều và hiểu rõ các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán và ứng dụng thực tế một cách dễ dàng. Hãy luyện tập thường xuyên để làm chủ kiến thức này.