Để chinh phục các bài toán về bất phương trình mũ, việc nắm vững cách tính tập nghiệm là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết về các phương pháp giải bất phương trình mũ, kèm theo các ví dụ minh họa và bài tập tự luyện để bạn có thể tự tin giải quyết mọi dạng bài tập.
1. Tổng Quan Về Bất Phương Trình Mũ
Bất phương trình mũ cơ bản có dạng: a^x > b (hoặc <, >=, <=), trong đó a, b là các số đã cho, a > 0 và a ≠ 1.
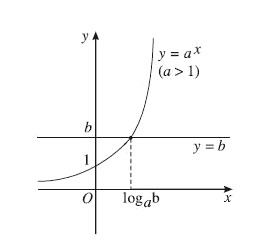
Để hiểu rõ hơn về tập nghiệm, ta có thể xem xét đồ thị của hàm số y = a^x và đường thẳng y = b.
Trường hợp 1: a > 1
- Nếu b ≤ 0:
a^x > bđúng với mọi x. - Nếu b > 0:
a^x > bkhi x > logab
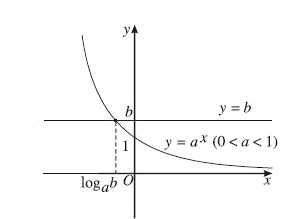
Trường hợp 2: 0 < a < 1
- Nếu b ≤ 0:
a^x > bđúng với mọi x. - Nếu b > 0:
a^x > bkhi x < logab
Ví dụ: Giải bất phương trình 3^(x^2 - x) < 9
- Ta có thể viết lại bất phương trình:
3^(x^2 - x) < 3^2 - Vì cơ số 3 > 1, ta suy ra:
x^2 - x < 2 - Giải bất phương trình bậc hai:
-1 < x < 2 - Vậy tập nghiệm của bất phương trình là (-1; 2).
2. Các Dạng Bất Phương Trình Mũ Thường Gặp và Cách Giải
Dưới đây là bảng tổng hợp các dạng bất phương trình mũ cơ bản và cách xác định tập nghiệm:
Dạng 1: ax > b (a > 0, a ≠ 1)
| Điều kiện | Nghiệm |
|---|---|
| a > 1 | b ≤ 0: R; b > 0: (logab; +∞) |
| 0 < a < 1 | b ≤ 0: R; b > 0: (-∞; logab) |
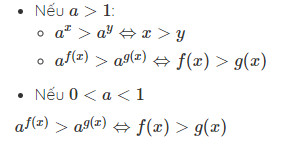



Dạng 2: ax ≥ b (a > 0, a ≠ 1)
| Điều kiện | Nghiệm |
|---|---|
| a > 1 | b ≤ 0: R; b > 0: [logab; +∞) |
| 0 < a < 1 | b ≤ 0: R; b > 0: (-∞; logab] |
Dạng 3: ax < b (a > 0, a ≠ 1)
| Điều kiện | Nghiệm |
|---|---|
| a > 1 | b ≤ 0: ∅; b > 0: (-∞; logab) |
| 0 < a < 1 | b ≤ 0: ∅; b > 0: (logab; +∞) |
Dạng 4: ax ≤ b (a > 0, a ≠ 1)
| Điều kiện | Nghiệm |
|---|---|
| a > 1 | b ≤ 0: ∅; b > 0: (-∞; logab] |
| 0 < a < 1 | b ≤ 0: ∅; b > 0: [logab; +∞) |
3. Các Phương Pháp Tính Tập Nghiệm Của Bất Phương Trình Mũ
3.1. Phương Pháp Đưa Về Cùng Cơ Số
Đây là phương pháp cơ bản nhất. Ta cố gắng biến đổi bất phương trình về dạng a^(f(x)) > a^(g(x)) (hoặc <, >=, <=).
- Nếu a > 1:
f(x) > g(x)(giữ nguyên chiều bất phương trình). - Nếu 0 < a < 1:
f(x) < g(x)(đổi chiều bất phương trình).
Đôi khi, ta cần sử dụng logarit để đưa về cùng cơ số:
Ví dụ 1: Giải bất phương trình 2^(x+1) > 8
- Ta có:
2^(x+1) > 2^3 - Vì 2 > 1:
x + 1 > 3=>x > 2 - Vậy tập nghiệm là (2; +∞).
Ví dụ 2: Giải bất phương trình (1/3)^(2x - 1) < 1/9
- Ta có:
(1/3)^(2x - 1) < (1/3)^2 - Vì 0 < 1/3 < 1:
2x - 1 > 2=>x > 3/2 - Vậy tập nghiệm là (3/2; +∞).
3.2. Phương Pháp Đặt Ẩn Phụ
Phương pháp này giúp đơn giản hóa bất phương trình, đưa về dạng quen thuộc hơn (thường là bất phương trình đại số).
Ví dụ: Giải bất phương trình 4^x - 3*2^x + 2 < 0
- Đặt
t = 2^x(t > 0). Bất phương trình trở thành:t^2 - 3t + 2 < 0 - Giải bất phương trình bậc hai:
1 < t < 2 - Thay
t = 2^x:1 < 2^x < 2=>2^0 < 2^x < 2^1 - Vì 2 > 1:
0 < x < 1 - Vậy tập nghiệm là (0; 1).
3.3. Phương Pháp Đánh Giá – Sử Dụng Tính Đơn Điệu
Phương pháp này thường được sử dụng cho các bất phương trình phức tạp, không thể giải bằng các phương pháp thông thường. Ta dựa vào tính đồng biến hoặc nghịch biến của hàm số mũ để đánh giá và tìm nghiệm.
- Hàm số
y = a^xđồng biến trên R khi a > 1. - Hàm số
y = a^xnghịch biến trên R khi 0 < a < 1.
Ví dụ: Giải bất phương trình 2^x + x > 3
- Xét hàm số
f(x) = 2^x + x. Hàm số này đồng biến trên R (tổng của hai hàm đồng biến). - Nhận thấy
f(1) = 2^1 + 1 = 3. - Vì f(x) đồng biến, nên
f(x) > 3khix > 1. - Vậy tập nghiệm là (1; +∞).
4. Bài Tập Luyện Tập
Hãy áp dụng các phương pháp trên để giải các bất phương trình sau:
5^(x-2) < 25(1/2)^(3x+1) >= 1/89^x - 4*3^x + 3 > 03^x + x^2 < 4
Lời khuyên:
- Nắm vững lý thuyết và các dạng bài tập cơ bản.
- Luyện tập thường xuyên để làm quen với các phương pháp giải.
- Khi gặp bài toán khó, hãy thử áp dụng nhiều phương pháp khác nhau để tìm ra lời giải.
Chúc các bạn học tốt và chinh phục thành công các bài toán về bất phương trình mũ!
