Tìm nguyên hàm là một trong những kỹ năng cơ bản và quan trọng trong giải tích. Trong bài viết này, chúng ta sẽ tập trung vào việc tìm nguyên hàm của hàm số đơn giản nhưng thường gặp: 3x. Bên cạnh đó, chúng ta sẽ mở rộng ra các dạng bài liên quan và các phương pháp giải hữu ích.
Trước hết, chúng ta cần nhớ lại định nghĩa cơ bản về nguyên hàm. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng (a; b) nếu F'(x) = f(x) với mọi x thuộc (a; b).
Vậy, Nguyên Hàm Của 3x là gì?
Hàm số cần tìm có dạng:
∫3x dx
Ta có thể đưa hằng số 3 ra ngoài dấu tích phân:
3∫x dx
Áp dụng công thức nguyên hàm của x^n, ta có ∫x dx = x²/2 + C
Vậy, nguyên hàm của 3x là: 3 * (x²/2) + C = (3/2)x² + C, trong đó C là hằng số tích phân.
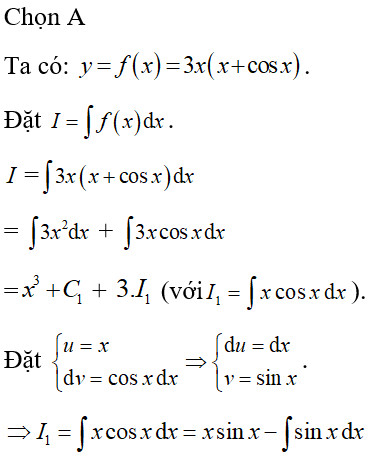Minh họa cách tính nguyên hàm của hàm số 3x
Có thể thấy, việc tìm nguyên hàm của 3x khá đơn giản, nhưng nó là nền tảng để giải quyết các bài toán phức tạp hơn. Việc nắm vững các công thức nguyên hàm cơ bản là vô cùng quan trọng.
Các Dạng Bài Tập Liên Quan Đến Nguyên Hàm của 3x
-
Tìm nguyên hàm của các hàm số đa thức: Đây là dạng bài cơ bản, yêu cầu áp dụng trực tiếp công thức nguyên hàm. Ví dụ: Tìm nguyên hàm của 3x + 2, 3x² + x + 1, …
-
Tìm nguyên hàm của các hàm số lượng giác: Dạng bài này đòi hỏi kiến thức về các công thức lượng giác và nguyên hàm của các hàm lượng giác cơ bản. Ví dụ: Tìm nguyên hàm của 3x cos(x), 3x sin(x), …
-
Tìm nguyên hàm bằng phương pháp đổi biến số: Phương pháp này thường được sử dụng khi biểu thức dưới dấu tích phân phức tạp. Ví dụ: Tìm nguyên hàm của 3x / (x² + 1), …
-
Tìm nguyên hàm bằng phương pháp tích phân từng phần: Phương pháp này thường được sử dụng khi biểu thức dưới dấu tích phân là tích của hai hàm số. Ví dụ: Tìm nguyên hàm của 3x * ln(x), …
Ví dụ Minh Họa:
Tìm họ nguyên hàm của hàm số y = 3x(x + cosx).
Đầu tiên ta khai triển biểu thức: y = 3x² + 3xcosx
Sau đó ta tìm nguyên hàm của từng thành phần:
∫3x² dx = x³ + C₁
∫3xcosx dx = 3∫xcosx dx
Để tính ∫xcosx dx, ta sử dụng phương pháp tích phân từng phần:
Đặt u = x, dv = cosx dx
=> du = dx, v = sinx
∫xcosx dx = xsinx – ∫sinx dx = xsinx + cosx + C₂
Vậy, ∫3xcosx dx = 3xsinx + 3cosx + C₂
Kết hợp lại, ta có họ nguyên hàm của y = 3x(x + cosx) là: x³ + 3xsinx + 3cosx + C (với C = C₁ + C₂)
Lưu ý khi giải bài tập nguyên hàm:
- Luôn nhớ cộng hằng số tích phân C vào kết quả.
- Kiểm tra lại kết quả bằng cách lấy đạo hàm của nguyên hàm vừa tìm, nếu đạo hàm bằng hàm số ban đầu thì kết quả đúng.
- Luyện tập thường xuyên để nắm vững các công thức và phương pháp giải.
Việc nắm vững kiến thức về nguyên hàm của 3x và các dạng bài liên quan sẽ giúp bạn tự tin hơn trong việc giải các bài toán tích phân phức tạp hơn. Chúc bạn thành công!
