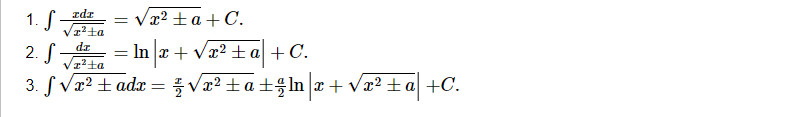Nguyên Hàm √x: Công Thức, Bài Tập và Phương Pháp Giải Chi Tiết

Trong chương trình giải tích, việc tìm nguyên hàm của các hàm số chứa căn thức, đặc biệt là Nguyên Hàm √x, là một kỹ năng quan trọng. Bài viết này sẽ cung cấp một cái nhìn tổng quan về nguyên hàm căn x, bao gồm công thức, các dạng bài tập thường gặp và phương pháp giải chi tiết.

Công Thức Tính Nguyên Hàm √x

Nguyên hàm của √x được xác định như sau:

∫√x dx = (2/3)x^(3/2) + C

Trong đó:

∫ là ký hiệu của phép tích phân (tìm nguyên hàm).
√x là hàm số cần tìm nguyên hàm.
(2/3)x^(3/2) là nguyên hàm của √x.
C là hằng số tích phân.

Các Dạng Bài Tập Về Nguyên Hàm √x Thường Gặp

Dưới đây là một số dạng bài tập phổ biến liên quan đến nguyên hàm √x và các phương pháp giải tương ứng:

1. Tìm Nguyên Hàm Bằng Phương Pháp Đổi Biến Số

Phương pháp đổi biến số là một kỹ thuật quan trọng để giải các bài toán nguyên hàm phức tạp. Ý tưởng chính là thay đổi biến số để đơn giản hóa biểu thức dưới dấu tích phân.

Ví dụ: Tìm nguyên hàm của hàm số ∫(5x-10)^0.5 dx

Lời giải:

Đặt u = 5x – 10, suy ra du = 5dx, hay dx = (1/5)du.

Khi đó, ∫(5x-10)^0.5 dx = ∫u^0.5 (1/5)du = (1/5) ∫u^0.5 du = (1/5) * (2/3)u^(3/2) + C = (2/15)(5x-10)^(3/2) + C

Vậy đáp án là (2/15)(5x-10)^(3/2) + C

2. Nguyên Hàm Các Hàm Số Chứa Căn Thức Dựa Trên Tam Thức Bậc Hai

Khi gặp các hàm số chứa căn thức và tam thức bậc hai, ta thường đưa tam thức về dạng chính tắc để đơn giản hóa bài toán.

Ví dụ: (Ví dụ cụ thể và lời giải chi tiết sẽ được bổ sung sau)

3. Tìm Nguyên Hàm Của Hàm Số f(x) = (x – ax + a) với a > 0

Với dạng bài này, ta có thể tách biểu thức thành các nguyên hàm đơn giản hơn.

(Ví dụ cụ thể và lời giải chi tiết sẽ được bổ sung sau)

4. Tìm Nguyên Hàm Của Hàm Số f(x) = dx / (ax + b + ax + c)

Để giải dạng này, ta thường khử tính vô tỉ ở mẫu số bằng cách trục căn thức.

Ví dụ: (Ví dụ cụ thể và lời giải chi tiết sẽ được bổ sung sau)

5. Tìm Nguyên Hàm Bằng Cách Sử Dụng Các Đồng Nhất Thức

Sử dụng các đồng nhất thức là một kỹ thuật quan trọng để đơn giản hóa biểu thức và tìm nguyên hàm.

Ví dụ: (Ví dụ cụ thể và lời giải chi tiết sẽ được bổ sung sau)

6. Tìm Nguyên Hàm Của Hàm Số: f(x) = v(x)dx / (u^2x ± a)

Phương pháp hằng số bất định thường được sử dụng trong trường hợp này.

Ví dụ: (Ví dụ cụ thể và lời giải chi tiết sẽ được bổ sung sau)

7. Tìm Nguyên Hàm Của Hàm Số: I=∫R(x,a^2+x^2).dx

(Phương pháp và ví dụ cụ thể sẽ được bổ sung sau)

8. Tìm Nguyên Hàm Của Hàm Số: I=∫R(x,x^2-a^2).dx

(Phương pháp và ví dụ cụ thể sẽ được bổ sung sau)