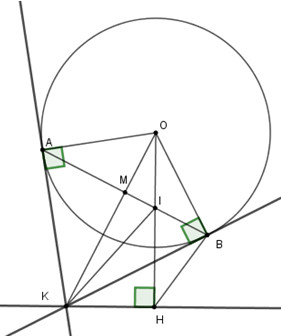
a) Chứng minh tứ giác OAKH nội tiếp
Vì (KA) là tiếp tuyến của (left( O right)) nên (AK bot OA Rightarrow angle KAO = 90^circ ).
Lại có (angle OHK = 90^circ ,,,(text{do},,OH bot d)).
Xét tứ giác (AOKH) có (angle OAK + angle OHK = 90^circ + 90^circ = 180^circ ) mà hai góc ở vị trí đối nhau nên tứ giác (OAKH) là tứ giác nội tiếp (dhnb).
b) Chứng minh 5 điểm A, O, B, H, K cùng thuộc một đường tròn và (IO.IH = IA.IB)
Xét (left( O right)) có (angle OBK = 90^circ ) (do (KB) là tiếp tuyến của đường tròn (left( O right))).
Từ đó ta có (angle OAK = ,angle OBK = angle OHK = 90^circ ) nên 5 điểm (A;O;B;H;K) cùng thuộc đường tròn đường kính (OK.)
(Rightarrow angle OAB = angle OHB) (hai góc nội tiếp cùng chắn cung (OB)).
Xét (Delta IOA) và (Delta IBH) có:
(angle OIA = angle BIH) (hai góc đối đỉnh)
(angle OAB = angle OHB) (cmt)
(begin{array}{l} Rightarrow Delta IOA sim Delta IBH,,,left( {g – g} right)\ Rightarrow frac{{IO}}{{IB}} = frac{{IA}}{{IH}} Leftrightarrow IO.IH = IA.IBend{array})
c) Chứng minh (OI = frac{{{R^2}}}{{OH}}) và suy ra (I) là điểm cố định
Xét đường tròn đường kính (OK) có:
(angle OHB) là góc nội tiếp chắn cung (OB)
(angle OBA) là góc nội tiếp chắn cung (OA)
Mà (OA = OB = R.)
(Rightarrow angle OHB = angle OBA) (hai góc nội tiếp chắn hai cung bằng nhau)
Xét (Delta OIB) và (Delta OBH) có
(begin{array}{l}angle BOH,,,,text{chung}\angle OHB = angle OBA,,,,,left( {cmt} right)end{array})
(begin{array}{l} Rightarrow Delta OIB sim Delta OBHleft( {g – g} right)\ Rightarrow frac{{OI}}{{OB}} = frac{{OB}}{{OH}} Leftrightarrow OI = frac{{O{B^2}}}{{OH}} = frac{{{R^2}}}{{OH}}end{array})
Mà đường thẳng (d) cố định nên (OH) không đổi (vì (OH bot d)).
(Rightarrow OI = frac{{{R^2}}}{{OH}}) không đổi hay điểm (I) cố định khi (K) chạy trên đường thẳng (d) cố định.
d) Tính diện tích tam giác KAI theo R
Gọi (M) là giao điểm của (OK) và (AB)
Xét đường tròn (left( O right)) có (KA,KB) là hai tiếp tuyến nên (KA = KB).
Lại có (OA = OB = R) nên (OK) là đường trung trực của (AB), suy ra (AB bot OK) tại (M.)
(Rightarrow {S_{Delta KAI}} = frac{1}{2}AI.KM.)
Theo câu b) ta có (OI = frac{{{R^2}}}{{OH}})(= frac{{{R^2}}}{{Rsqrt 3 }} = frac{R}{{sqrt 3 }})
Xét tam giác (OAK) vuông tại (A,) theo hệ thức lượng trong tam giác vuông ta có:
+) (O{A^2} = OM.OK Leftrightarrow OM = frac{{O{A^2}}}{{OK}} = frac{{{R^2}}}{{2R}} = frac{R}{2}.)
Suy ra (KM = OK – OM = 2R – frac{R}{2} = frac{{3R}}{2}.)
+) (A{M^2} = OM.KM = frac{R}{2}.frac{{3R}}{2} = frac{{3{R^2}}}{4} Rightarrow AM = frac{{Rsqrt 3 }}{2}.)
Xét tam giác (OMI) vuông tại (M), theo định lý Pytago ta có:
(MI = sqrt {O{I^2} – O{M^2}} = sqrt {{{left( {frac{R}{{sqrt 3 }}} right)}^2} – {{left( {frac{R}{2}} right)}^2}} = frac{{Rsqrt 3 }}{6})
Suy ra (AI = AM + MI = frac{{Rsqrt 3 }}{2} + frac{{Rsqrt 3 }}{6} = frac{{2Rsqrt 3 }}{3})
(Rightarrow {S_{Delta KAI}} = frac{1}{2}KM.AI = frac{1}{2}.frac{{3R}}{2}.frac{{2Rsqrt 3 }}{3} = frac{{{R^2}sqrt 3 }}{2}) .
Vậy ({S_{Delta KAI}} = frac{{{R^2}sqrt 3 }}{2}.)