Trong toán học, giới hạn của dãy số là một khái niệm nền tảng, đặc biệt quan trọng khi làm việc với các dãy số vô hạn. Việc xác định “Lim N Bằng Bao Nhiêu” thực chất là việc tìm hiểu xem dãy số có hội tụ về một giá trị cụ thể hay không, và nếu có, giá trị đó là bao nhiêu.
1. Giới Hạn Hữu Hạn
Một dãy số (uₙ) có giới hạn hữu hạn là a (ký hiệu lim uₙ = a khi n tiến đến vô cùng) nếu, với mọi số dương bé tùy ý, tồn tại một số N sao cho với mọi n > N, |uₙ – a| nhỏ hơn số dương đó. Nói một cách đơn giản, các số hạng của dãy số ngày càng tiến gần đến giá trị a khi n trở nên rất lớn.
+) lim uₙ = 0 (khi n tiến đến vô cùng) khi và chỉ khi |uₙ| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
+) lim uₙ = a ⇔ lim (uₙ – a) = 0 (khi n tiến đến vô cùng).
2. Giới Hạn Vô Cực
Không phải dãy số nào cũng có giới hạn hữu hạn. Một số dãy số có giới hạn vô cực, tức là các số hạng của dãy số tăng hoặc giảm không giới hạn khi n tiến đến vô cùng.
+) lim uₙ = +∞ (khi n tiến đến vô cùng) khi và chỉ khi uₙ có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
+) lim uₙ = -∞ ⇔ lim(-uₙ) = +∞ (khi n tiến đến vô cùng).
3. Các Giới Hạn Đặc Biệt
Một số giới hạn đặc biệt thường gặp và hữu ích trong việc tính toán giới hạn của các dãy số phức tạp hơn:
a) lim (1/n) = 0;
lim (1/nᵏ) = 0;
lim nᵏ = +∞, với k nguyên dương.b) lim qⁿ = 0 nếu |q| < 1;
lim qⁿ = +∞ nếu q > 1.
c) lim c = c (c là hằng số).
4. Định Lí Về Giới Hạn Hữu Hạn
Các định lý này cho phép chúng ta tính toán giới hạn của các biểu thức phức tạp bằng cách chia nhỏ chúng thành các phần đơn giản hơn:
a) Nếu lim uₙ = a và lim vₙ = b, thì:
lim (uₙ + vₙ) = a + b
lim (uₙ – vₙ) = a – b
lim (uₙ.vₙ) = ab
lim (uₙ / vₙ) = a / b (nếu b ≠ 0).
b) Nếu uₙ ≥ 0 với mọi n và lim uₙ = a thì a > 0 và lim √uₙ = √a.
5. Định Lí Liên Hệ Giữa Giới Hạn Hữu Hạn và Giới Hạn Vô Cực.
Những định lý này hữu ích khi một phần của biểu thức có giới hạn hữu hạn, trong khi phần còn lại có giới hạn vô cực:
a) Nếu lim uₙ = a và lim vₙ = ± ∞ thì lim (uₙ / vₙ) = 0.
b) Nếu lim uₙ = a > 0, lim vₙ = 0 và vₙ > 0 với mọi n thì lim (uₙ / vₙ) = +∞
c) Nếu lim uₙ = +∞ và lim vₙ = a > 0 thì lim (uₙ.vₙ) = +∞.
6. Cấp Số Nhân Lùi Vô Hạn
Cấp số nhân lùi vô hạn là một trường hợp đặc biệt, nơi công bội q có giá trị tuyệt đối nhỏ hơn 1 (|q| < 1). Tổng của cấp số nhân lùi vô hạn có thể được tính bằng công thức đơn giản:
+) Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội q thỏa mãn |q| < 1
+) Công thức tính tổng S của cấp số lùi vô hạn (uₙ):
S = u₁ + u₂ + … + uₙ + … = u₁ / (1 – q)
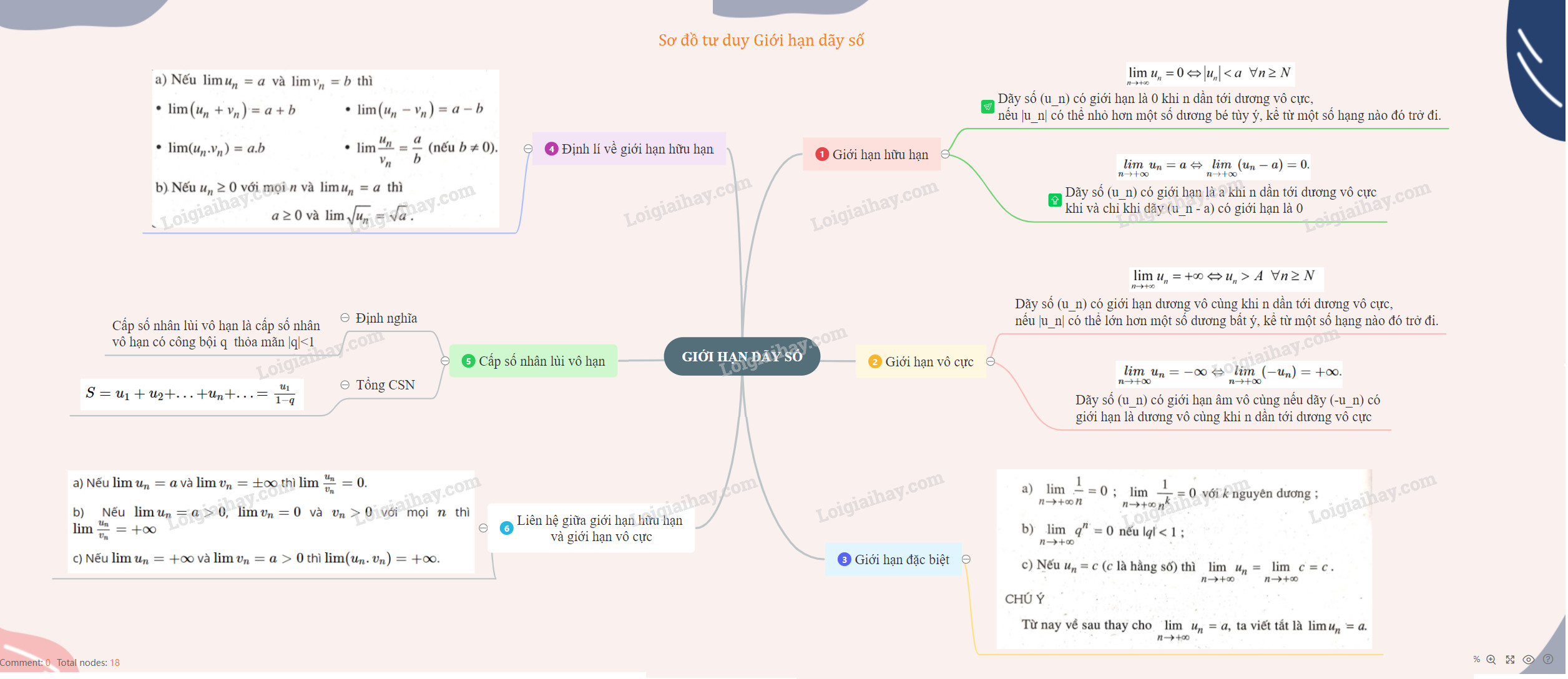Sơ đồ tư duy giới hạn dãy số trực quan giúp hệ thống hóa kiến thức về lim n.
Hiểu rõ các khái niệm và định lý về giới hạn, đặc biệt là việc “lim n bằng bao nhiêu” trong các trường hợp khác nhau, là chìa khóa để giải quyết nhiều bài toán phức tạp trong giải tích và các lĩnh vực liên quan.
