Hệ Tọa độ Descartes, một công cụ toán học mạnh mẽ, đóng vai trò then chốt trong nhiều lĩnh vực, từ hình học giải tích đến thiết kế đồ họa và các ứng dụng kỹ thuật. Vậy hệ tọa độ Descartes là gì và tại sao nó lại quan trọng đến vậy? Bài viết này sẽ đi sâu vào khám phá hệ tọa độ Descartes, lịch sử hình thành, các khái niệm cơ bản và ứng dụng thực tế của nó trong thế giới hiện đại.
Hệ Tọa Độ Descartes Là Gì? Lịch Sử Hình Thành
Hệ tọa độ Descartes (Cartesian coordinate system) cho phép xác định vị trí của một điểm trên mặt phẳng hoặc trong không gian bằng cách sử dụng các số tọa độ. Trên mặt phẳng, một điểm được xác định bởi cặp số (x, y), trong đó x và y lần lượt là khoảng cách đến hai trục vuông góc giao nhau tại một điểm gốc gọi là gốc tọa độ.
Cha đẻ của hệ tọa độ Descartes là nhà toán học và triết học người Pháp, René Descartes (1596-1650). Hệ tọa độ này được giới thiệu lần đầu tiên trong các tác phẩm của ông vào thế kỷ 17, đặc biệt là trong “Phương pháp luận” (Discours de la méthode) và “Hình học” (La Géométrie). Ý tưởng đột phá của Descartes là tạo ra một mối liên hệ giữa đại số và hình học, cho phép biểu diễn các hình học bằng các phương trình đại số và ngược lại. Đây là nền tảng của hình học giải tích, một nhánh quan trọng của toán học hiện đại.
Giải Thích Các Thuật Ngữ Quan Trọng Trong Hệ Tọa Độ Descartes
Để hiểu rõ hơn về hệ tọa độ Descartes, chúng ta cần nắm vững một số thuật ngữ cơ bản:
- Trục tọa độ: Là tập hợp các đường thẳng vuông góc với nhau, thường là hai trục (trục hoành Ox và trục tung Oy) trong không gian hai chiều, hoặc ba trục (Ox, Oy, Oz) trong không gian ba chiều.
- Trục hoành (Ox): Là đường thẳng nằm ngang, thường được sử dụng để biểu diễn giá trị x.
- Trục tung (Oy): Là đường thẳng thẳng đứng, thường được sử dụng để biểu diễn giá trị y.
- Trục cao (Oz): Là đường thẳng vuông góc với cả trục Ox và Oy, sử dụng trong không gian ba chiều để biểu diễn giá trị z.
- Gốc tọa độ (O): Là điểm giao nhau của các trục tọa độ, có tọa độ (0, 0) trong không gian hai chiều và (0, 0, 0) trong không gian ba chiều.
- Mặt phẳng tọa độ: Là mặt phẳng được tạo bởi hai trục tọa độ, ví dụ mặt phẳng Oxy, Oxz, Oyz trong không gian ba chiều.
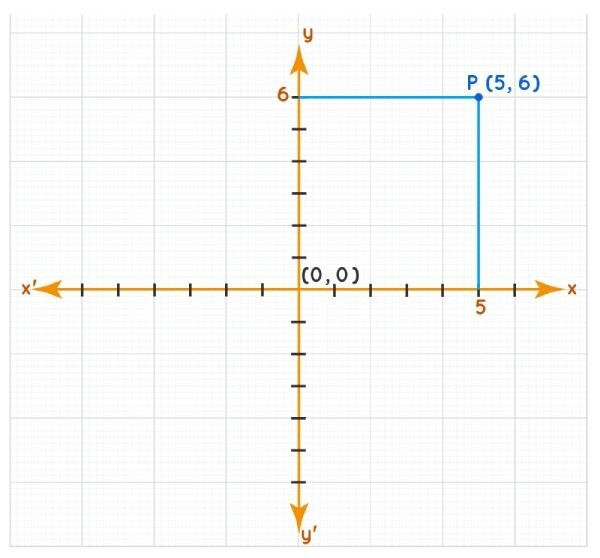
- Tọa độ của một điểm: Là bộ các số xác định vị trí của điểm đó trong hệ tọa độ. Ví dụ, điểm P(x, y) có tọa độ x và y lần lượt là khoảng cách từ P đến trục Oy và Ox.
Hình ảnh minh họa vị trí của một điểm P(x, y) bất kỳ trên hệ tọa độ Descartes hai chiều, với x là hoành độ và y là tung độ.
Các Hệ Trục Tọa Độ Descartes Thường Gặp
Hệ tọa độ Descartes có thể được mở rộng sang nhiều chiều, nhưng phổ biến nhất là hệ tọa độ một chiều, hai chiều và ba chiều.
Hệ Tọa Độ Descartes Một Chiều
Hệ tọa độ một chiều chỉ bao gồm một trục số, thường là trục số thực. Vị trí của một điểm trên trục này được xác định bởi một số duy nhất, biểu thị khoảng cách từ điểm đó đến gốc tọa độ (thường là số 0). Hệ tọa độ một chiều thường được sử dụng để biểu diễn các đại lượng có thể được đo lường trên một đường thẳng, chẳng hạn như nhiệt độ, thời gian, hoặc vị trí trên một đường ray.
Hệ Tọa Độ Descartes Hai Chiều (2D)
Hệ tọa độ hai chiều, hay còn gọi là mặt phẳng tọa độ, bao gồm hai trục vuông góc là trục hoành (Ox) và trục tung (Oy). Mặt phẳng này được chia thành bốn góc phần tư, được đánh số từ I đến IV theo chiều ngược chiều kim đồng hồ, bắt đầu từ góc phần tư phía trên bên phải. Mỗi điểm trên mặt phẳng được xác định bởi một cặp số (x, y), trong đó x là hoành độ và y là tung độ.
Giá trị của các điểm trên các góc phần tư được xác định như sau:
- Góc phần tư thứ nhất (I): x > 0, y > 0
- Góc phần tư thứ hai (II): x < 0, y > 0
- Góc phần tư thứ ba (III): x < 0, y < 0
- Góc phần tư thứ tư (IV): x > 0, y < 0
Hệ Tọa Độ Descartes Ba Chiều (3D)
Hệ tọa độ ba chiều được tạo thành từ ba trục vuông góc là trục hoành (Ox), trục tung (Oy) và trục cao (Oz). Ba trục này giao nhau tại gốc tọa độ (O) và chia không gian thành tám phần được gọi là “bát phân”. Mỗi điểm trong không gian ba chiều được xác định bởi bộ ba số (x, y, z), trong đó x, y, và z lần lượt là khoảng cách từ điểm đó đến các mặt phẳng Oyz, Oxz, và Oxy.
Hình ảnh minh họa hệ tọa độ Descartes ba chiều, thể hiện rõ ba trục vuông góc Ox (hoành độ), Oy (tung độ), và Oz (cao độ) và cách xác định vị trí một điểm trong không gian.
Ứng Dụng Thực Tế Của Hệ Tọa Độ Descartes
Hệ tọa độ Descartes có vô số ứng dụng trong nhiều lĩnh vực khác nhau, bao gồm:
- Toán học: Nền tảng của hình học giải tích, giúp biểu diễn các đường thẳng, đường cong, mặt phẳng và các hình học phức tạp khác bằng các phương trình đại số.
- Vật lý: Sử dụng để mô tả chuyển động của các vật thể trong không gian, tính toán lực, và xây dựng các mô hình vật lý.
- Kỹ thuật: Ứng dụng trong thiết kế và xây dựng, từ việc vẽ bản vẽ kỹ thuật đến lập trình cho máy CNC.
- Thiết kế đồ họa: Cơ sở cho việc tạo ra các hình ảnh và mô hình 3D trên máy tính, sử dụng trong phim ảnh, trò chơi điện tử và thiết kế sản phẩm.
- Địa lý: Sử dụng trong hệ thống thông tin địa lý (GIS) để lưu trữ, phân tích và hiển thị dữ liệu không gian.
- Định vị toàn cầu (GPS): Hệ thống GPS sử dụng hệ tọa độ ba chiều để xác định vị trí của các thiết bị trên Trái Đất.
- Trí tuệ nhân tạo (AI) và Khoa học dữ liệu: Ứng dụng trong biểu diễn dữ liệu đa chiều, phân tích không gian, và xây dựng các mô hình học máy.
Những Lưu Ý Quan Trọng Về Hệ Tọa Độ Descartes
Khi sử dụng hệ tọa độ Descartes, cần lưu ý một số điểm sau:
- Gốc tọa độ là điểm tham chiếu quan trọng, mọi vị trí đều được xác định so với gốc tọa độ.
- Trục tọa độ phải vuông góc với nhau (trong hệ tọa độ vuông góc Descartes).
- Thứ tự của các tọa độ rất quan trọng, ví dụ điểm (x, y) khác với điểm (y, x).
- Có thể mở rộng hệ tọa độ Descartes sang nhiều chiều hơn ba, nhưng khó hình dung trực quan.
Kết Luận
Hệ tọa độ Descartes là một công cụ toán học vô cùng mạnh mẽ và linh hoạt, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học, kỹ thuật và công nghệ. Từ việc giải quyết các bài toán hình học phức tạp đến việc xây dựng các mô hình 3D và định vị toàn cầu, hệ tọa độ Descartes đã và đang góp phần quan trọng vào sự phát triển của xã hội hiện đại. Việc nắm vững các khái niệm cơ bản và ứng dụng của hệ tọa độ Descartes là rất quan trọng đối với bất kỳ ai muốn theo đuổi sự nghiệp trong các lĩnh vực liên quan đến toán học, khoa học, kỹ thuật và công nghệ.