Phân số thập phân là một dạng phân số đặc biệt và rất quan trọng trong toán học, đặc biệt khi làm việc với số thập phân. Bài viết này sẽ giúp bạn hiểu rõ cách chuyển đổi phân số thường thành phân số thập phân một cách dễ dàng và hiệu quả.
1. Thế nào là phân số thập phân?
Phân số thập phân là phân số có mẫu số là lũy thừa của 10, ví dụ: 10, 100, 1000, 10000,…
Ví dụ: $frac{3}{10}$, $frac{25}{100}$, $frac{123}{1000}$ là các phân số thập phân.
2. Tại sao cần chuyển đổi phân số thành phân số thập phân?
Việc chuyển đổi phân số thành phân số thập phân giúp chúng ta dễ dàng so sánh, cộng, trừ các phân số, và đặc biệt là chuyển đổi chúng thành số thập phân một cách nhanh chóng.
3. Các phương pháp chuyển phân số thành phân số thập phân
Có hai phương pháp chính để chuyển đổi một phân số thành phân số thập phân:
-
Phương pháp 1: Nhân hoặc chia cả tử và mẫu số
Mục tiêu của phương pháp này là biến đổi mẫu số của phân số ban đầu thành 10, 100, 1000,… Để làm được điều này, ta cần tìm một số thích hợp để nhân hoặc chia cả tử số và mẫu số.
-
Ví dụ 1: Chuyển phân số $frac{2}{5}$ thành phân số thập phân.
Ta thấy 5 có thể nhân với 2 để được 10. Vậy ta nhân cả tử và mẫu của phân số $frac{2}{5}$ với 2:
$frac{2}{5} = frac{2 times 2}{5 times 2} = frac{4}{10}$
Vậy $frac{2}{5}$ = $frac{4}{10}$
-
-
Ví dụ 2: Chuyển phân số $frac{16}{40}$ thành phân số thập phân.
Ta thấy 40 có thể chia cho 4 để được 10. Vậy ta chia cả tử và mẫu của phân số $\frac{16}{40}$ cho 4: $\frac{16}{40} = \frac{16 : 4}{40 : 4} = \frac{4}{10}$ Vậy $\frac{16}{40}$ = $\frac{4}{10}$ -
Phương pháp 2: Sử dụng phép chia
Trong trường hợp không thể dễ dàng tìm được số để nhân hoặc chia, ta có thể thực hiện phép chia tử số cho mẫu số. Nếu kết quả là một số thập phân hữu hạn, ta có thể dễ dàng chuyển nó thành phân số thập phân.
4. Các ví dụ minh họa
Ví dụ 1: Viết các phân số sau thành phân số thập phân: $frac{3}{2};frac{2}{5}$
Giải:
- $frac{3}{2} = frac{3 times 5}{2 times 5} = frac{15}{10}$
- $frac{2}{5} = frac{2 times 2}{5 times 2} = frac{4}{10}$
Ví dụ 2: Viết các phân số sau thành phân số thập phân: $frac{{17}}{{20}};frac{{63}}{{50}}$
Giải:
- $frac{17}{20} = frac{17 times 5}{20 times 5} = frac{85}{100}$
- $frac{63}{50} = frac{63 times 2}{50 times 2} = frac{126}{100}$
Ví dụ 3: Viết các phân số sau thành phân số thập phân: $frac{{33}}{{500}};frac{{147}}{{250}}$
Giải:
- $frac{33}{500} = frac{33 times 2}{500 times 2} = frac{66}{1000}$
- $frac{147}{250} = frac{147 times 4}{250 times 4} = frac{588}{1000}$
5. Bài tập vận dụng
Để nắm vững kiến thức, hãy cùng làm một số bài tập sau:
Bài 1: Trong các phân số sau, phân số nào là phân số thập phân?
Bài 2: Các phân số nào dưới đây là phân số thập phân?
Alt: Xác định phân số thập phân trong các phân số đã cho, mẫu số là lũy thừa của 10
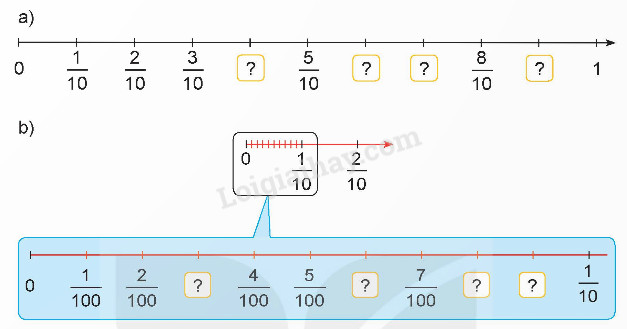
Bài 3: Tìm phân số thập phân thích hợp.
Alt: Điền phân số thích hợp vào chỗ trống để hoàn thành dãy phân số thập phân
Bài 4: Số?
Alt: Tìm số thích hợp để phân số trở thành phân số thập phân tương đương
Bài 5: Số?
Alt: Tìm giá trị thích hợp để hoàn thành phép biến đổi phân số thành phân số thập phân
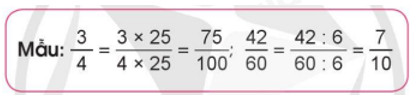
Bài 6: Chuyển các phân số sau thành phân số thập phân (theo mẫu):
a) $frac{2}{5},,frac{7}{4},,frac{{18}}{{25}}$
b) $frac{{32}}{{80}},,frac{{72}}{{400}},,frac{{425}}{{5,000}}$
Alt: Chuyển đổi các phân số thành phân số thập phân bằng cách nhân hoặc chia tử và mẫu số
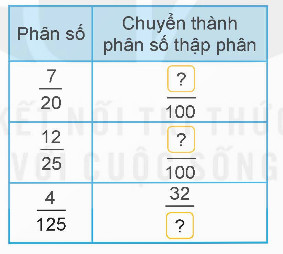
Bài 7: Viết số thích hợp vào chỗ chấm
| Phân số | Chuyển thành phân số thập phân |
|---|---|
| (frac{9}{{20}}) | (frac{{}}{{100}}) |
| (frac{{12}}{{300}}) | (frac{{}}{{100}}) |
| (frac{7}{{125}}) | (frac{{56}}{{}}) |


Alt: Hoàn thành bảng chuyển đổi phân số thành phân số thập phân bằng cách điền số thích hợp
6. Ứng dụng của phân số thập phân
Phân số thập phân có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực:
- Tính toán: Giúp đơn giản hóa các phép tính liên quan đến phân số.
- Đo lường: Sử dụng trong các đơn vị đo lường như mét, centimet, milimet,…
- Tài chính: Tính toán lãi suất, phần trăm, chiết khấu,…
7. Kết luận
Việc nắm vững cách chuyển đổi phân số thành phân số thập phân là một kỹ năng quan trọng trong toán học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và bài tập hữu ích để bạn có thể tự tin giải quyết các bài toán liên quan đến phân số thập phân. Chúc các bạn học tốt!
