1. Động Lượng: Khái Niệm Cơ Bản
Động lượng là một đại lượng vật lý quan trọng mô tả “lượng vận động” của một vật. Nó được định nghĩa là tích của khối lượng (m) và vận tốc ((overrightarrow{v})) của vật. Công thức tính động lượng là:
(overrightarrow{p}=moverrightarrow{v})
Động lượng là một đại lượng vectơ, có hướng trùng với hướng của vận tốc. Đơn vị đo của động lượng trong hệ SI là kg.m/s.
2. Xung Lượng của Lực: Thay Đổi Động Lượng
Xung lượng của lực là đại lượng đặc trưng cho tác dụng của lực trong một khoảng thời gian nhất định. Khi một lực (overrightarrow{F}) tác dụng lên một vật trong khoảng thời gian ∆t, xung lượng của lực được tính bằng công thức:
(overrightarrow{J} = overrightarrow{F}Delta t)
Đơn vị của xung lượng là N.s. Xung lượng của lực gây ra sự thay đổi động lượng của vật. Mối liên hệ giữa xung lượng và động lượng được thể hiện qua định lý xung lượng – động lượng:
(Delta overrightarrow{p} = overrightarrow{J}) hay (Delta overrightarrow{p} = overrightarrow{F}Delta t)
3. Hệ Cô Lập: Điều Kiện Để Bảo Toàn Động Lượng
Một hệ vật được gọi là hệ cô lập (hay hệ kín) khi không có ngoại lực tác dụng lên hệ, hoặc khi tổng các ngoại lực tác dụng lên hệ bằng không. Nói cách khác, các lực tương tác giữa các vật trong hệ là nội lực, và chúng không làm thay đổi tổng động lượng của hệ.
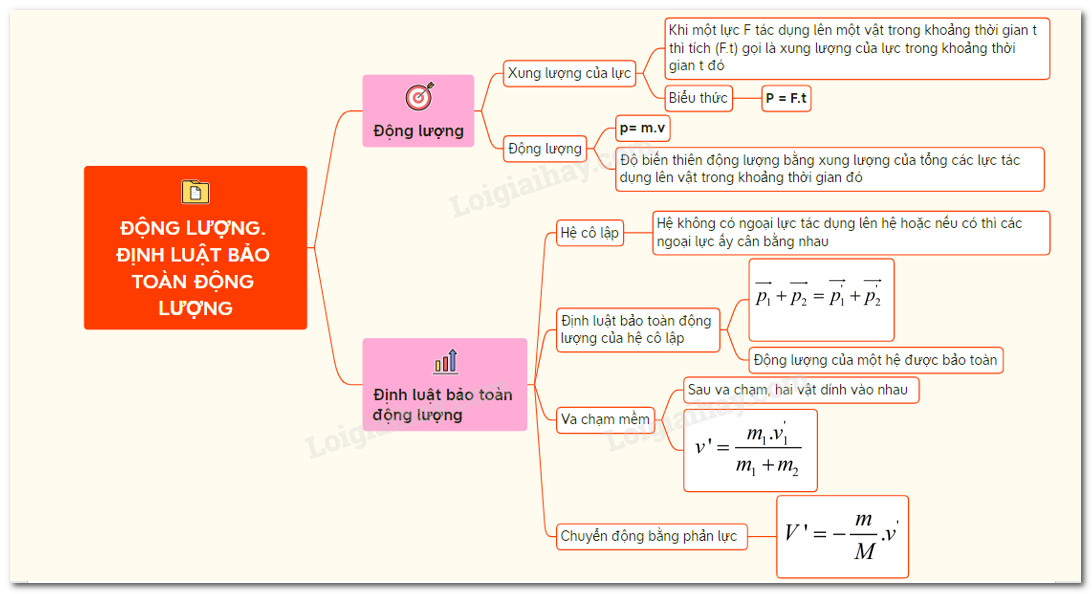Hệ cô lập: Các lực tác dụng lên hệ cân bằng lẫn nhau, đảm bảo động lượng được bảo toàn.
Hệ cô lập: Các lực tác dụng lên hệ cân bằng lẫn nhau, đảm bảo động lượng được bảo toàn. Alt text này tối ưu SEO với từ khóa “hệ cô lập”, “động lượng bảo toàn”, và mô tả chính xác nội dung ảnh.
4. Định Luật Bảo Toàn Động Lượng: Nền Tảng Của Vật Lý
Động lượng của một hệ cô lập là một đại lượng bảo toàn. Đây là một trong những định luật cơ bản và quan trọng nhất của vật lý. Điều này có nghĩa là tổng động lượng của hệ không đổi theo thời gian, bất kể các tương tác xảy ra bên trong hệ.
(overrightarrow{p_{hệ}} = overrightarrow{p_1} + overrightarrow{p_2} + … + overrightarrow{p_n} = const.)
Định luật bảo toàn động lượng có nhiều ứng dụng quan trọng trong việc giải quyết các bài toán vật lý, đặc biệt là trong các bài toán về va chạm, chuyển động bằng phản lực.
5. Ứng Dụng Của Định Luật Bảo Toàn Động Lượng
5.1. Va Chạm
Trong các vụ va chạm giữa các vật, động lượng của hệ kín (gồm các vật va chạm) được bảo toàn. Có hai loại va chạm chính:
- Va chạm đàn hồi: Động năng của hệ được bảo toàn.
- Va chạm mềm (va chạm không đàn hồi): Động năng của hệ không được bảo toàn (một phần động năng chuyển thành nhiệt hoặc các dạng năng lượng khác).
Ví dụ, trong va chạm mềm, sau va chạm các vật dính vào nhau và chuyển động cùng vận tốc. Áp dụng định luật bảo toàn động lượng, ta có:
(m_1 overrightarrow{v_1} + m_2 overrightarrow{v_2} = (m_1 + m_2) overrightarrow{v})
trong đó (overrightarrow{v}) là vận tốc chung của hai vật sau va chạm.
5.2. Chuyển Động Bằng Phản Lực
Chuyển động bằng phản lực là một ứng dụng quan trọng khác của định luật bảo toàn động lượng. Ví dụ điển hình là chuyển động của tên lửa. Khi tên lửa phóng ra khí nóng về phía sau, nó nhận được một xung lượng ngược chiều, đẩy tên lửa tiến về phía trước. Theo định luật bảo toàn động lượng:
(moverrightarrow{v} + Moverrightarrow{V} = overrightarrow{0})
trong đó m là khối lượng khí phụt ra, (overrightarrow{v}) là vận tốc của khí, M là khối lượng tên lửa, và (overrightarrow{V}) là vận tốc của tên lửa.
Tên lửa đẩy: Ứng dụng định luật bảo toàn động lượng trong chuyển động bằng phản lực, tạo lực đẩy tiến cho tên lửa bằng cách phụt khí ra phía sau. Alt text tập trung vào “tên lửa đẩy”, “định luật bảo toàn động lượng”, “chuyển động bằng phản lực”, tối ưu cho tìm kiếm liên quan đến vật lý và kỹ thuật.
5.3. Các Ví Dụ Thực Tế Khác
Định luật bảo toàn động lượng còn được ứng dụng trong nhiều lĩnh vực khác, chẳng hạn như:
- Súng giật khi bắn: Khi bắn súng, viên đạn bay về phía trước, súng giật lùi về phía sau để bảo toàn động lượng.
- Đi bộ: Khi bạn bước đi, bạn đẩy chân về phía sau, và theo định luật bảo toàn động lượng, bạn tiến về phía trước.
6. Bài Tập Vận Dụng
Bài 1: Một viên bi khối lượng 0.5 kg đang chuyển động với vận tốc 2 m/s va chạm mềm với một viên bi khác có khối lượng 1 kg đang đứng yên. Tính vận tốc của hai viên bi sau va chạm.
Giải:
Áp dụng định luật bảo toàn động lượng:
(m_1overrightarrow{v_1} + m_2overrightarrow{v_2} = (m_1 + m_2)overrightarrow{v})
Vì viên bi thứ hai đứng yên, nên (overrightarrow{v_2} = 0). Do đó:
(0.5 2 = (0.5 + 1) v)
(v = frac{1}{1.5} = frac{2}{3} approx 0.67 m/s)
Vậy vận tốc của hai viên bi sau va chạm là khoảng 0.67 m/s.
Bài 2: Một người khối lượng 60 kg nhảy ra khỏi một chiếc thuyền khối lượng 120 kg đang đứng yên trên mặt nước với vận tốc 3 m/s so với thuyền. Tính vận tốc của thuyền ngay sau khi người nhảy ra.
Giải:
Áp dụng định luật bảo toàn động lượng:
(m_1overrightarrow{v_1} + m_2overrightarrow{v_2} = overrightarrow{0}) (vì ban đầu hệ đứng yên)
(60 3 + 120 v_2 = 0)
(v_2 = -frac{180}{120} = -1.5 m/s)
Vậy vận tốc của thuyền ngay sau khi người nhảy ra là -1.5 m/s (ngược chiều với hướng nhảy của người).
7. Kết Luận
Động lượng và định luật bảo toàn động lượng là những khái niệm và định luật quan trọng trong vật lý, có nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật. Việc hiểu rõ và vận dụng thành thạo các kiến thức này sẽ giúp bạn giải quyết nhiều bài toán vật lý phức tạp và khám phá thế giới xung quanh một cách sâu sắc hơn.
