Bảng Biến Thiên Hàm Số: Bí Quyết Chinh Phục Bài Toán Khảo Sát Hàm Số

Bảng Biến Thiên Hàm Số là một công cụ vô cùng quan trọng trong việc khảo sát và vẽ đồ thị hàm số. Nó giúp ta xác định được các khoảng đồng biến, nghịch biến, cực trị của hàm số một cách trực quan và dễ dàng. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và sâu sắc về bảng biến thiên hàm số, đặc biệt tập trung vào hàm số bậc hai, cùng với các ví dụ minh họa và bài tập thực hành để bạn nắm vững kiến thức này.

1. Tổng Quan Về Bảng Biến Thiên Hàm Số

Bảng biến thiên là một bảng tóm tắt thông tin về sự biến thiên của hàm số trên tập xác định. Thông thường, bảng biến thiên bao gồm các hàng sau:

Hàng thứ nhất: Giá trị của biến số x (bao gồm các điểm đặc biệt như điểm cực trị, điểm không xác định).
Hàng thứ hai: Giá trị của đạo hàm f'(x).
Hàng thứ ba: Chiều biến thiên của hàm số (đồng biến, nghịch biến) và các giá trị cực trị (nếu có).
Hàng thứ tư: Giá trị của hàm số f(x) tại các điểm tương ứng.

2. Bảng Biến Thiên Hàm Số Bậc Hai

Hàm số bậc hai có dạng tổng quát là y = ax² + bx + c, trong đó a, b, c là các hằng số và a ≠ 0. Việc lập bảng biến thiên cho hàm số bậc hai là một kỹ năng cơ bản và quan trọng.

2.1. Các Bước Lập Bảng Biến Thiên

Xác định tập xác định: Tập xác định của hàm số bậc hai luôn là D = ℝ (tập hợp tất cả các số thực).
Tính đạo hàm: Tính đạo hàm của hàm số: y’ = 2ax + b.
Tìm nghiệm của đạo hàm: Giải phương trình y’ = 0 để tìm nghiệm. Nghiệm này là x = -b/2a, đây chính là hoành độ đỉnh của parabol.
Xác định dấu của đạo hàm:
- Nếu a > 0: y’ < 0 khi x < -b/2a (hàm số nghịch biến), y’ > 0 khi x > -b/2a (hàm số đồng biến).
- Nếu a < 0: y’ > 0 khi x < -b/2a (hàm số đồng biến), y’ < 0 khi x > -b/2a (hàm số nghịch biến).
Lập bảng biến thiên: Dựa vào các thông tin trên, ta lập bảng biến thiên.

2.2. Dạng Bảng Biến Thiên

Trường hợp a > 0:
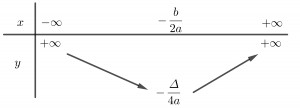
Trường hợp a < 0:

3. Ví Dụ Minh Họa

Ví dụ 1: Lập bảng biến thiên của hàm số y = x² – 4x + 3.

Giải:
- a = 1 > 0.
- y’ = 2x – 4.
- y’ = 0 <=> x = 2.
- Giá trị của hàm số tại x = 2 là y = 2² – 4*2 + 3 = -1.
Vậy bảng biến thiên là:

Ví dụ 2: Lập bảng biến thiên của hàm số y = -x² + 2x + 1.

Giải:
- a = -1 < 0.
- y’ = -2x + 2.
- y’ = 0 <=> x = 1.
- Giá trị của hàm số tại x = 1 là y = -1² + 2*1 + 1 = 2.
Vậy bảng biến thiên là:

4. Ứng Dụng Của Bảng Biến Thiên

Bảng biến thiên là một công cụ hữu ích trong nhiều bài toán liên quan đến hàm số, bao gồm:

Tìm cực trị của hàm số: Bảng biến thiên cho phép xác định trực quan các điểm cực đại và cực tiểu của hàm số.
Xác định khoảng đồng biến, nghịch biến: Dựa vào bảng biến thiên, ta có thể dễ dàng xác định các khoảng mà hàm số tăng hoặc giảm.
Vẽ đồ thị hàm số: Bảng biến thiên cung cấp thông tin quan trọng để vẽ đồ thị hàm số một cách chính xác.
Giải các bài toán liên quan đến sự tương giao: Bảng biến thiên giúp xác định số lượng nghiệm của phương trình f(x) = m (với m là tham số).

5. Bài Tập Thực Hành

Bài 1: Lập bảng biến thiên của hàm số y = 2x² + 4x – 1.

Bài 2: Lập bảng biến thiên của hàm số y = -3x² + 6x + 2.

Bài 3: Cho hàm số y = x² – 2mx + m² – 1. Lập bảng biến thiên và tìm m để hàm số đồng biến trên khoảng (1; +∞).

6. Mẹo Nhỏ Khi Lập Bảng Biến Thiên

Kiểm tra lại dấu của đạo hàm: Sau khi tìm được nghiệm của đạo hàm, hãy kiểm tra lại dấu của đạo hàm trên các khoảng để đảm bảo tính chính xác.
Tính toán cẩn thận: Việc tính toán sai có thể dẫn đến bảng biến thiên không chính xác.
Vẽ phác đồ thị: Sau khi lập bảng biến thiên, hãy vẽ phác đồ thị hàm số để kiểm tra lại tính hợp lý của bảng biến thiên.

7. Kết Luận

Bảng biến thiên là một công cụ mạnh mẽ giúp ta hiểu rõ hơn về sự biến thiên của hàm số. Việc nắm vững cách lập và sử dụng bảng biến thiên sẽ giúp bạn giải quyết các bài toán liên quan đến hàm số một cách hiệu quả. Hãy luyện tập thường xuyên để thành thạo kỹ năng này. Chúc bạn thành công!