Tia Phân Giác Trong Tam Giác Vuông là một chủ đề quan trọng trong hình học. Bài viết này sẽ cung cấp đầy đủ kiến thức về định nghĩa, tính chất, và các dạng bài tập liên quan đến tia phân giác trong tam giác vuông, giúp bạn nắm vững kiến thức và giải quyết các bài toán hiệu quả.
I. Định Nghĩa và Tính Chất Cơ Bản
1. Định nghĩa:
Trong một tam giác vuông, tia phân giác của một góc là tia xuất phát từ đỉnh của góc đó và chia góc đó thành hai góc bằng nhau. Tia phân giác trong tam giác vuông có những đặc điểm và tính chất riêng biệt.
2. Tính Chất Quan Trọng:
- Tính chất 1: Mọi điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
- Tính chất 2: Điểm nằm trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Những tính chất này rất quan trọng trong việc chứng minh và giải các bài toán liên quan đến tia phân giác.
II. Các Dạng Bài Tập Thường Gặp
Dạng 1: Tính độ dài các đoạn thẳng liên quan đến tia phân giác
Bài tập dạng này thường yêu cầu tính độ dài các đoạn thẳng mà tia phân giác chia cạnh đối diện thành. Để giải quyết, chúng ta thường sử dụng tính chất của đường phân giác trong tam giác: tỉ lệ giữa các đoạn thẳng mà nó tạo ra trên cạnh đối diện.
Ví dụ 1: Tam giác ABC có AB = 6cm, AC = 9cm, BC = 10cm, đường phân giác trong AD. Tính độ dài DB.
Lời giải:
Áp dụng tính chất đường phân giác AD trong tam giác ABC, ta có:
DB/DC = AB/AC
DB/(BC - DB) = 6/9
DB/(10 - DB) = 2/3
3DB = 20 - 2DB
5DB = 20
DB = 4 cm
Dạng 2: Chứng minh các tính chất hình học sử dụng tia phân giác
Trong dạng bài này, bạn cần chứng minh các tính chất về góc, cạnh, hoặc mối quan hệ giữa các yếu tố hình học khác bằng cách sử dụng tính chất của tia phân giác.
Ví dụ 2: Cho tam giác ABC cân tại A, AB = 10cm, BC = 12cm. Gọi I là giao điểm các đường phân giác của tam giác. Tính độ dài AI.
Dạng 3: Ứng dụng tia phân giác để giải bài toán thực tế
Một số bài toán thực tế có thể được giải quyết bằng cách áp dụng kiến thức về tia phân giác trong tam giác. Điều này giúp chúng ta hiểu rõ hơn về tính ứng dụng của hình học trong cuộc sống.
Ví dụ 3: Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
Lời giải:
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
AB/BC = AD/DC = 4/5
Đặt AB = 4t và BC = 5t (với t > 0)
Áp dụng định lý Pytago cho tam giác ABC vuông tại A:
BC^2 = AC^2 + AB^2
(5t)^2 = (4 + 5)^2 + (4t)^2
25t^2 = 81 + 16t^2
9t^2 = 81
t^2 = 9
t = 3 (vì t > 0)
Khi đó: AB = 4 3 = 12 cm, BC = 5 3 = 15 cm
III. Bài Tập Vận Dụng
Dưới đây là một số bài tập để bạn luyện tập và củng cố kiến thức về tia phân giác trong tam giác vuông:
Bài 1: Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
Bài 2: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là bao nhiêu?
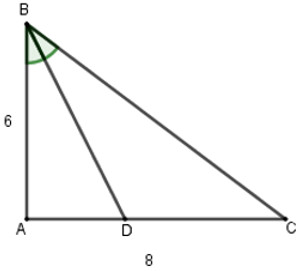Hình vẽ tam giác ABC vuông tại A, phân giác góc B cắt AC tại D.
Bài 3: Cho tam giác ABC, AB = 15cm, AC = 20cm, đường cao AH (H thuộc BC). Tia phân giác của góc BAH cắt HB tại D. Tính DH.
Bài 4: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D. Tính BC, DB, DC.
Bài 5: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 6 cm. Gọi E là trung điểm AC, tia phân giác của góc A cắt BC tại D. Chứng minh rằng: điểm D cách đều AB và AC.
.png)
IV. Kết Luận
Hiểu rõ về tia phân giác trong tam giác vuông là rất quan trọng để giải quyết nhiều bài toán hình học. Bằng cách nắm vững lý thuyết, tính chất và luyện tập các dạng bài tập khác nhau, bạn sẽ tự tin hơn trong việc chinh phục các bài toán hình học liên quan. Chúc bạn học tốt!
