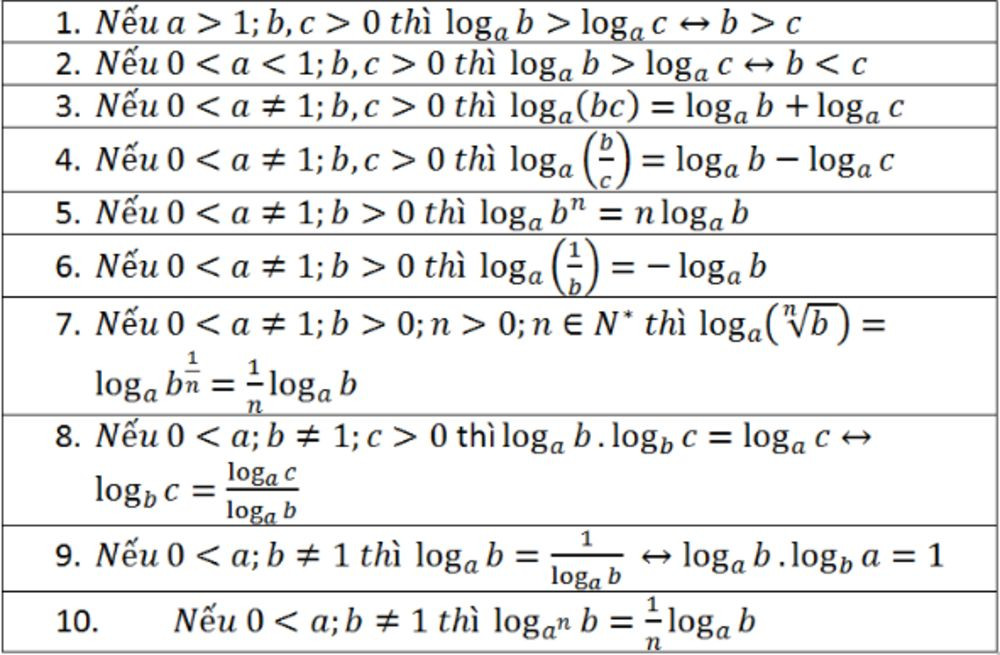Logarit là một phần kiến thức toán học quan trọng trong chương trình phổ thông, đóng vai trò then chốt trong nhiều bài toán và kỳ thi. Để nắm vững và áp dụng hiệu quả, học sinh cần hiểu rõ về Tính Chất Logarit, các công thức liên quan và cách giải các dạng bài tập thường gặp.
Logarit Là Gì?
Logarit là phép toán nghịch đảo của lũy thừa. Hiểu một cách đơn giản, logarit của một số là số mũ mà cơ số (một giá trị cố định) cần được nâng lên để tạo ra số đó.
Ví dụ: 2³ = 8, vậy logarit cơ số 2 của 8 là 3 (ký hiệu: log₂8 = 3).
Logarit được sử dụng để tính toán phép nhân của hai số dương bất kỳ, trong đó một số khác 1. Lũy thừa cho phép các số dương có thể nâng lên lũy thừa với số mũ bất kỳ để nhận về kết quả là một số dương.
Tính Chất Logarit Cơ Bản
Tính chất logarit là nền tảng để giải các bài toán liên quan đến hàm số logarit. Các tính chất này chỉ áp dụng khi cơ số và đối số là số dương, và cơ số khác 0 và 1.
Bảng tổng hợp các tính chất logarit quan trọng, bao gồm logarit của tích, thương, lũy thừa và căn, giúp học sinh dễ dàng tra cứu và áp dụng vào giải bài tập.
Dưới đây là bảng tổng hợp các tính chất logarit quan trọng:
- logₐ1 = 0 (Logarit của 1 luôn bằng 0)
- logₐa = 1 (Logarit của cơ số bằng 1)
- logₐ(xy) = logₐx + logₐy (Logarit của một tích bằng tổng các logarit)
- logₐ(x/y) = logₐx – logₐy (Logarit của một thương bằng hiệu các logarit)
- logₐ(xⁿ) = n * logₐx (Logarit của một lũy thừa)
- a^(logₐx) = x (Công thức cơ bản về lũy thừa của logarit)
Bảng Công Thức Logarit Chi Tiết
Để giải quyết các bài toán phức tạp hơn, học sinh cần nắm vững bảng công thức logarit đầy đủ, bao gồm:
1. Công Thức Logarit Cơ Bản
2. Công Thức Lũy Thừa Logarit
3. Công Thức Logarit và Các Phép Toán
4. Công Thức Đổi Cơ Số
5. Công Thức Đạo Hàm Logarit
- Hàm cơ bản: (logₐx)’ = 1/(x * ln(a))
- Hàm hợp: (logₐu(x))’ = u'(x) / (u(x) * ln(a))
Các Quy Tắc Quan Trọng Về Logarit
Nắm vững các quy tắc sau giúp áp dụng tính chất logarit một cách chính xác:
- Quy tắc logarit của lũy thừa: logₐ(b^α) = αlogₐb
- Quy tắc logarit của một tích: logₐ(ab) = logₐa + logₐb
Lưu Ý Khi Học và Sử Dụng Công Thức Logarit
- Phân biệt hàm số mũ và logarit: Phương trình logarit có chứa “log”, trong khi phương trình mũ có biến số ở số mũ.
- Nhớ các thành phần của công thức logarit: log, cơ số, đối số.
- Phân biệt các loại logarit: Logarit thập phân (cơ số 10), logarit tự nhiên (cơ số e).
Hình ảnh minh họa các lưu ý quan trọng, nhấn mạnh sự khác biệt giữa các loại logarit và cách áp dụng công thức chính xác.
Để học và ghi nhớ công thức đạo hàm logarit một cách hiệu quả, hãy:
- Nắm vững kiến thức cơ bản về logarit và các công thức liên quan.
- Luyện tập giải các bài tập trong sách giáo khoa và sách nâng cao.
- Trao đổi với bạn bè và thầy cô giáo để hiểu sâu hơn về vấn đề.
- Tham khảo các nguồn thông tin uy tín trên mạng để mở rộng kiến thức.
Cách Giải Một Số Dạng Bài Tập Logarit Thường Gặp
Dạng 1: So sánh các biểu thức chứa logarit
- Bước 1: Sử dụng tính chất logarit để đơn giản hóa các biểu thức.
- Bước 2: So sánh các biểu thức đã đơn giản, sử dụng các tính chất so sánh logarit.
Dạng 2: Biểu diễn một logarit qua các logarit đã cho
- Bước 1: Sử dụng các tính chất logarit để tách biểu thức cần biểu diễn thành các logarit theo yêu cầu.
- Bước 2: Thay các dữ liệu đề bài cho và rút gọn biểu thức.
Dạng 3: Rút gọn biểu thức logarit
- Bước 1: Chuyển đổi các logarit về cùng một cơ số.
- Bước 2: Rút gọn các logarit cùng cơ số theo các quy tắc.
Nắm vững tính chất logarit, các công thức liên quan và phương pháp giải các dạng bài tập thường gặp là chìa khóa để thành công trong học tập và các kỳ thi. Chúc các bạn học tốt!