Bài viết này sẽ cung cấp kiến thức toàn diện về tam giác đồng dạng, một chủ đề quan trọng trong chương trình toán lớp 7. Chúng ta sẽ cùng tìm hiểu về định nghĩa, các trường hợp đồng dạng, tính chất và cách chứng minh tam giác đồng dạng thông qua các ví dụ minh họa và bài tập luyện tập.
1. Định Nghĩa Tam Giác Đồng Dạng
Hai tam giác được gọi là đồng dạng nếu chúng có hình dạng giống nhau, nhưng kích thước có thể khác nhau. Nói cách khác, các góc tương ứng của hai tam giác bằng nhau, và các cạnh tương ứng tỉ lệ với nhau.
Cho hai tam giác ABC và A’B’C’. Ta nói tam giác ABC đồng dạng với tam giác A’B’C’ (ký hiệu là ΔABC ∼ ΔA’B’C’) nếu:
- Các góc: ∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’
- Tỉ lệ các cạnh: AB/A’B’ = BC/B’C’ = CA/C’A’
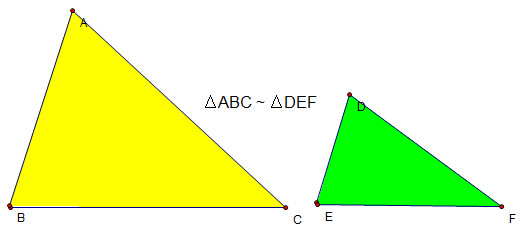
Minh họa hai tam giác đồng dạng ABC và A’B’C’, nhấn mạnh sự tương ứng giữa các cạnh và góc để học sinh lớp 7 dễ hình dung khái niệm.
2. Các Trường Hợp Đồng Dạng Của Tam Giác (Lớp 7)
Trong chương trình toán lớp 7, chúng ta tập trung vào ba trường hợp đồng dạng cơ bản của tam giác:
2.1. Trường Hợp Cạnh – Cạnh – Cạnh (c.c.c)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia, thì hai tam giác đó đồng dạng.
Ví dụ: Cho ΔABC có AB = 4cm, BC = 6cm, CA = 8cm và ΔDEF có DE = 2cm, EF = 3cm, FD = 4cm. Ta có:
AB/DE = 4/2 = 2
BC/EF = 6/3 = 2
CA/FD = 8/4 = 2
Vì AB/DE = BC/EF = CA/FD nên ΔABC ∼ ΔDEF (c.c.c).
2.2. Trường Hợp Cạnh – Góc – Cạnh (c.g.c)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc xen giữa hai cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Ví dụ: Cho ΔMNP có MN = 5cm, MP = 7cm, ∠M = 50° và ΔQRS có QR = 10cm, QS = 14cm, ∠Q = 50°. Ta có:
MN/QR = 5/10 = 1/2
MP/QS = 7/14 = 1/2
∠M = ∠Q = 50°
Vì MN/QR = MP/QS và ∠M = ∠Q nên ΔMNP ∼ ΔQRS (c.g.c).
2.3. Trường Hợp Góc – Góc (g.g)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia, thì hai tam giác đó đồng dạng.
Ví dụ: Cho ΔABC có ∠A = 60°, ∠B = 80° và ΔDEF có ∠D = 60°, ∠E = 80°. Ta có:
∠A = ∠D = 60°
∠B = ∠E = 80°
Vì ∠A = ∠D và ∠B = ∠E nên ΔABC ∼ ΔDEF (g.g).
3. Tính Chất Của Tam Giác Đồng Dạng
Khi hai tam giác đồng dạng, chúng có những tính chất quan trọng sau:
- Tỉ số các đường cao tương ứng bằng tỉ số đồng dạng.
- Tỉ số các đường trung tuyến tương ứng bằng tỉ số đồng dạng.
- Tỉ số các đường phân giác tương ứng bằng tỉ số đồng dạng.
- Tỉ số chu vi của hai tam giác bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác bằng bình phương tỉ số đồng dạng.
4. Bài Tập Về Tam Giác Đồng Dạng
Việc luyện tập giải bài tập là rất quan trọng để nắm vững kiến thức về tam giác đồng dạng. Dưới đây là một số ví dụ và bài tập luyện tập:
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng ΔABH ∼ ΔCBA.
Hướng dẫn:
- ∠AHB = ∠BAC = 90°
- ∠B chung
=> ΔABH ∼ ΔCBA (g.g)
Bài tập 2: Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Chứng minh rằng ΔAOB ∼ ΔCOD.
Hướng dẫn:
- ∠AOB = ∠COD (đối đỉnh)
- ∠OAB = ∠OCD (so le trong)
=> ΔAOB ∼ ΔCOD (g.g)
Hình ảnh tổng hợp các phương pháp chứng minh hai tam giác đồng dạng thường gặp trong chương trình lớp 7, giúp học sinh ôn tập và hệ thống kiến thức.
Bài tập 3: Cho ΔABC có AB = 6cm, AC = 9cm, BC = 12cm. Trên cạnh AB lấy điểm D sao cho AD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 3cm. Chứng minh rằng ΔADE ∼ ΔABC.
Hướng dẫn:
- AD/AB = 2/6 = 1/3
- AE/AC = 3/9 = 1/3
- ∠A chung
=> ΔADE ∼ ΔABC (c.g.c)
Bài tập 4: (Bài tập nâng cao) Cho tam giác ABC, gọi D là trung điểm của BC. Qua D kẻ đường thẳng song song với AB, cắt AC ở E. Qua E kẻ đường thẳng song song với BC, cắt AB ở F. Chứng minh rằng:
a) Tứ giác BDEF là hình bình hành.
b) AE = EF
Bài tập 5: (Bài tập nâng cao) Cho tam giác ABC vuông tại A có AB
a) Chứng minh: ΔAHB ~ ΔCHA
b) Tính các đoạn AC, HB, HC.
Hy vọng qua bài viết này, các em học sinh lớp 7 đã nắm vững kiến thức về tam giác đồng dạng và có thể áp dụng để giải các bài tập liên quan. Chúc các em học tốt!