Hàm số logarit là một khái niệm quan trọng trong toán học. Bài viết này sẽ cung cấp đầy đủ kiến thức về đạo Hàm Của Logarit, từ định nghĩa, công thức, đến các dạng bài tập thường gặp, giúp bạn nắm vững và áp dụng thành thạo.
Để hiểu rõ hơn về đạo hàm logarit, hãy cùng điểm qua những kiến thức cơ bản về hàm số logarit và đạo hàm.
1. Kiến Thức Nền Tảng: Hàm Số Logarit và Đạo Hàm
1.1. Đạo Hàm: Định Nghĩa và Ý Nghĩa
Đạo hàm của một hàm số tại một điểm thể hiện tốc độ thay đổi tức thời của hàm số đó tại điểm đó.
- Định nghĩa: Đạo hàm của hàm số y = f(x) tại x₀ là giới hạn của tỉ số giữa số gia của hàm số và số gia của đối số khi số gia của đối số tiến dần đến 0.
- Ký hiệu: y'(x₀) hoặc f'(x₀).
- Ý nghĩa: Đạo hàm cho biết chiều biến thiên và độ lớn của sự biến thiên của hàm số tại một điểm.
1.2. Các Quy Tắc Đạo Hàm Cơ Bản
Để tính đạo hàm của hàm logarit, cần nắm vững các quy tắc đạo hàm sau:
- (u + v)’ = u’ + v’
- (u – v)’ = u’ – v’
- (u.v)’ = u’.v + u.v’
- (u/v)’ = (u’.v – u.v’) / v²
- (ku)’ = ku’ (với k là hằng số)
- Đạo hàm của hàm hợp: Nếu y = f(u) và u = g(x) thì y'(x) = y'(u) u'(x)*.
1.3. Hàm Số Logarit: Định Nghĩa, Tập Xác Định và Đồ Thị
- Định nghĩa: Hàm số logarit cơ số a của x (với a > 0 và a ≠ 1) là hàm số y = logₐ(x).
- Tập xác định: D = (0; +∞).
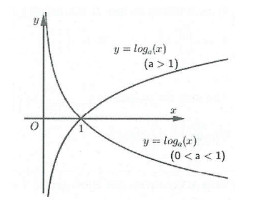
- Đồ thị: Đồ thị hàm số logarit luôn đi qua điểm (1; 0) và có tiệm cận đứng là trục Oy.
2. Đạo Hàm của Logarit: Công Thức và Tính Chất
2.1. Công Thức Đạo Hàm Logarit Cơ Bản
- Đạo hàm của logₐ(x): (logₐ(x))’ = 1 / (x * ln(a))
- Trường hợp đặc biệt (logarit tự nhiên): (ln(x))’ = 1/x
2.2. Công Thức Đạo Hàm Logarit Tổng Quát
- Đạo hàm của logₐ(u(x)): (logₐ(u(x)))’ = u'(x) / (u(x) * ln(a))
- Trường hợp đặc biệt (logarit tự nhiên): (ln(u(x)))’ = u'(x) / u(x)
2.3. Tính Chất Liên Quan Đến Đạo Hàm Logarit
- Nếu a > 1 thì (logₐ(x))’ > 0, hàm số đồng biến trên khoảng (0; +∞).
- Nếu 0 < a < 1 thì (logₐ(x))’ < 0, hàm số nghịch biến trên khoảng (0; +∞).
2.4. Bảng Tổng Hợp Công Thức Đạo Hàm Logarit
3. Các Dạng Bài Tập Về Đạo Hàm Logarit và Ví Dụ Minh Họa
3.1. Dạng 1: Tính Đạo Hàm Trực Tiếp
Ví dụ: Tính đạo hàm của hàm số y = ln(x² + 1)
Giải:
Áp dụng công thức đạo hàm của hàm logarit hợp:
y’ = (x² + 1)’ / (x² + 1) = 2x / (x² + 1)
3.2. Dạng 2: Tính Đạo Hàm Của Hàm Số Phức Tạp Chứa Logarit
Ví dụ: Tính đạo hàm của hàm số y = x ln(x)*
Giải:
Áp dụng công thức đạo hàm của tích:
y’ = (x)’ ln(x) + x (ln(x))’ = 1 ln(x) + x (1/x) = ln(x) + 1
Kết Luận
Nắm vững lý thuyết và công thức về đạo hàm logarit là chìa khóa để giải quyết các bài toán liên quan. Hãy luyện tập thường xuyên với các dạng bài tập khác nhau để nâng cao kỹ năng và đạt kết quả tốt trong học tập.