1. Định nghĩa
Trong hình học không gian, đường thẳng được gọi là vuông góc với mặt phẳng khi và chỉ khi nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Đây là khái niệm cơ bản nhất để xác định mối quan hệ vuông góc giữa đường thẳng và mặt phẳng.
Định lý 1: Để chứng minh một đường thẳng vuông góc với một mặt phẳng, ta chỉ cần chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó.
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh còn lại của tam giác đó.
2. Tính chất
Tính chất 1: Cho một điểm O và một đường thẳng a, tồn tại duy nhất một mặt phẳng (P) đi qua điểm O và vuông góc với đường thẳng a.
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với AB tại trung điểm O của đoạn thẳng đó.
3. Liên hệ giữa quan hệ song song và quan hệ vuông góc
Tính chất 3:
a) Nếu một mặt phẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 5:
a) Cho đường thẳng a và mặt phẳng (P) song song với nhau. Nếu một đường thẳng vuông góc với (P) thì nó cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
4. Phép chiếu vuông góc
Định nghĩa:
Phép chiếu song song lên mặt phẳng (P) theo phương l vuông góc với mặt phẳng (P) được gọi là phép chiếu vuông góc lên mặt phẳng (P). Phép chiếu vuông góc là một công cụ quan trọng để giải các bài toán hình học không gian.
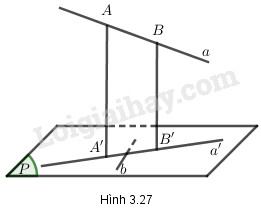
Định lý ba đường vuông góc:
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). Điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P). Định lý này là một công cụ mạnh mẽ để chứng minh các quan hệ vuông góc trong không gian.
5. Góc giữa đường thẳng và mặt phẳng
Định nghĩa:
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa a và (P) bằng 90 độ.
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
Chú ý: Góc giữa đường thẳng và mặt phẳng luôn nhỏ hơn hoặc bằng 90 độ.
Ứng dụng thực tế:
Khái niệm đường thẳng vuông góc với mặt phẳng có rất nhiều ứng dụng trong thực tế, ví dụ như trong xây dựng (đảm bảo các cột trụ vuông góc với nền nhà), trong thiết kế kỹ thuật (đảm bảo các chi tiết máy móc hoạt động chính xác), và trong nhiều lĩnh vực khác. Việc hiểu rõ và vận dụng thành thạo các kiến thức về đường thẳng vuông góc với mặt phẳng là rất quan trọng trong học tập và công việc.