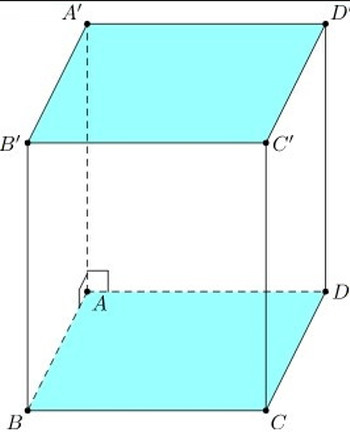
Hình lăng trụ là một khái niệm quan trọng trong hình học không gian, đặc biệt là Khối Lăng Trụ Tứ Giác đều. Bài viết này sẽ cung cấp một cái nhìn toàn diện về hình lăng trụ tứ giác đều, từ định nghĩa cơ bản đến các tính chất đặc trưng và ứng dụng thực tế.
Định Nghĩa Hình Lăng Trụ Tứ Giác Đều
Hình lăng trụ tứ giác đều là một trường hợp đặc biệt của hình lăng trụ đứng, trong đó:
- Đáy là một hình vuông.
- Các cạnh bên vuông góc với mặt đáy.
Điều này có nghĩa là tất cả các mặt bên của khối lăng trụ tứ giác đều là các hình chữ nhật bằng nhau và các mặt đáy là hai hình vuông đồng nhất.
Tính Chất Quan Trọng của Lăng Trụ Tứ Giác Đều
Khối lăng trụ tứ giác đều sở hữu những tính chất hình học đặc biệt, giúp chúng ta dễ dàng tính toán và ứng dụng:
-
Hai đáy là hình vuông: Hai mặt đáy của lăng trụ là hai hình vuông hoàn toàn giống nhau và song song với nhau.
-
Các mặt bên là hình chữ nhật: Bốn mặt bên đều là hình chữ nhật và có diện tích bằng nhau.
-
Các cạnh bên bằng nhau và vuông góc với đáy: Các cạnh bên có độ dài bằng nhau và tạo thành góc vuông với mặt phẳng đáy.
-
Tính đối xứng: Hình lăng trụ tứ giác đều có tính đối xứng cao, với nhiều mặt phẳng đối xứng và trục đối xứng.
Công Thức Tính Toán Liên Quan Đến Lăng Trụ Tứ Giác Đều
Để giải các bài toán liên quan đến lăng trụ tứ giác đều, chúng ta cần nắm vững các công thức sau:
- Diện tích đáy (Sđ): Vì đáy là hình vuông, nên Sđ = a², trong đó ‘a’ là độ dài cạnh đáy.
- Diện tích xung quanh (Sxq): Sxq = 4ah, trong đó ‘a’ là cạnh đáy và ‘h’ là chiều cao của lăng trụ (độ dài cạnh bên).
- Diện tích toàn phần (Stp): Stp = Sxq + 2Sđ = 4ah + 2a²
- Thể tích (V): V = Sđ * h = a²h
Ví Dụ Minh Họa
Bài toán: Cho một hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy a = 5cm và chiều cao h = 10cm. Tính diện tích toàn phần và thể tích của lăng trụ.
Giải:
- Diện tích đáy: Sđ = 5² = 25 cm²
- Diện tích xung quanh: Sxq = 4 5 10 = 200 cm²
- Diện tích toàn phần: Stp = 200 + 2 * 25 = 250 cm²
- Thể tích: V = 25 * 10 = 250 cm³
Ứng Dụng Thực Tế
Khối lăng trụ tứ giác đều xuất hiện rất nhiều trong đời sống hàng ngày và trong các lĩnh vực kỹ thuật:
- Kiến trúc và xây dựng: Các tòa nhà, cột trụ, và các cấu trúc khác thường có dạng hình lăng trụ tứ giác đều để đảm bảo tính vững chắc và thẩm mỹ.
- Thiết kế sản phẩm: Nhiều sản phẩm gia dụng, đồ nội thất, và các thiết bị công nghiệp có hình dạng lăng trụ tứ giác đều vì tính tiện dụng và khả năng tối ưu hóa không gian.
- Toán học và giáo dục: Lăng trụ tứ giác đều là một hình mẫu quan trọng trong việc giảng dạy và học tập hình học không gian, giúp học sinh phát triển tư duy logic và khả năng hình dung.
Bài Tập Vận Dụng
- Một hình lăng trụ tứ giác đều có thể tích là 1000 cm³ và cạnh đáy là 10cm. Tính chiều cao của lăng trụ.
- Tính diện tích xung quanh của một khối lăng trụ tứ giác đều có cạnh đáy là 6cm và đường chéo của mặt bên là 10cm.
- Một bể nước hình lăng trụ tứ giác đều không nắp có cạnh đáy 2m và chiều cao 1.5m. Tính diện tích vật liệu cần để xây bể (bỏ qua mạch vữa).
Kết Luận
Hình lăng trụ tứ giác đều là một hình học quan trọng với nhiều ứng dụng thực tế. Việc nắm vững định nghĩa, tính chất, và các công thức tính toán liên quan sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và hiểu rõ hơn về thế giới xung quanh.