Hàm số bậc nhất là một trong những khái niệm cơ bản và quan trọng trong chương trình toán học phổ thông. Việc nắm vững kiến thức về hàm số bậc nhất không chỉ giúp học sinh giải quyết các bài toán liên quan mà còn là nền tảng để tiếp cận các khái niệm toán học phức tạp hơn. Bài viết này sẽ đi sâu vào tìm hiểu về hàm số bậc nhất, đặc biệt tập trung vào dạng của nó, cùng với các dạng bài tập thường gặp và phương pháp giải.
1. Dạng Tổng Quát của Hàm Số Bậc Nhất
Hàm Số Bậc Nhất Có Dạng tổng quát là:
y = ax + b
Trong đó:
xlà biến số độc lập.ylà biến số phụ thuộc, giá trị của nó phụ thuộc vàox.avàblà các hằng số, vớia ≠ 0.ađược gọi là hệ số góc vàblà tung độ gốc.
Khi b = 0, hàm số bậc nhất có dạng đặc biệt:
y = ax
Đây là trường hợp hàm số biểu thị mối quan hệ tỉ lệ thuận giữa y và x.
Đồ thị hàm số y=ax thể hiện mối quan hệ tỉ lệ thuận giữa y và x.
Tính chất quan trọng:
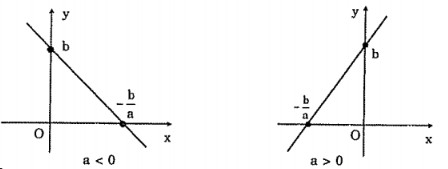
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc tập số thực R và có các tính chất sau:
- Đồng biến trên R nếu a > 0: Khi
xtăng,ycũng tăng. - Nghịch biến trên R nếu a < 0: Khi
xtăng,ygiảm.
2. Các Dạng Bài Tập Cơ Bản và Cách Giải
2.1. Xác Định Hàm Số Bậc Nhất
Đây là dạng bài tập yêu cầu xác định xem một hàm số cho trước có phải là hàm số bậc nhất hay không. Để giải quyết dạng bài tập này, cần kiểm tra xem hàm số có thể viết được về dạng y = ax + b với a ≠ 0 hay không.
Ví dụ: Với điều kiện nào của m thì các hàm số sau đây là hàm số bậc nhất?
a) y = (m - 1)x + m
b) y = (m² - 2x - 3)x² + (m + 1)x + m
c) y = √(m² - 1) . x + 2
Hướng dẫn giải:
a) y = (m - 1)x + m là hàm số bậc nhất khi và chỉ khi m - 1 ≠ 0, tức là m ≠ 1.
b) y = (m² - 2x - 3)x² + (m + 1)x + m là hàm số bậc nhất khi m² - 2x - 3 = 0 và m + 1 ≠ 0. Giải phương trình và bất phương trình này để tìm giá trị của m.
c) y = √(m² - 1) . x + 2 là hàm số bậc nhất khi và chỉ khi √(m² - 1) ≠ 0, tức là m² - 1 > 0. Điều này xảy ra khi m > 1 hoặc m < -1.
2.2. Tìm Điều Kiện để Hàm Số Đồng Biến hoặc Nghịch Biến
Dạng bài tập này yêu cầu tìm các giá trị của tham số để hàm số bậc nhất đồng biến hoặc nghịch biến trên tập số thực R. Để giải quyết dạng bài tập này, cần dựa vào dấu của hệ số a trong công thức y = ax + b.
Ví dụ: Tìm a để các hàm số dưới đây:
a) y = (a + 2)x + 3 đồng biến trên R.
b) y = (m² - m)x + m nghịch biến trên R.
Hướng dẫn giải:
a) y = (a + 2)x + 3 đồng biến trên R khi và chỉ khi a + 2 > 0, tức là a > -2.
b) y = (m² - m)x + m nghịch biến trên R khi và chỉ khi m² - m < 0, tức là 0 < m < 1.
Ví dụ minh họa về sự đồng biến của hàm số bậc nhất.
3. Đồ Thị Hàm Số Bậc Nhất
Đồ thị của hàm số bậc nhất y = ax + b là một đường thẳng. Để vẽ đồ thị của hàm số bậc nhất, ta có thể thực hiện theo các bước sau:
- Xác định hai điểm phân biệt thuộc đồ thị: Có thể chọn hai giá trị bất kỳ của
xvà tính giá trị tương ứng củay. Hoặc có thể tìm giao điểm của đồ thị với hai trục tọa độ. - Vẽ đường thẳng đi qua hai điểm đã xác định.
Ví dụ: Vẽ đồ thị hàm số y = x + 2.
Hướng dẫn giải:
- Chọn
x = 0, ta cóy = 2. Vậy điểm (0; 2) thuộc đồ thị. - Chọn
x = -1, ta cóy = 1. Vậy điểm (-1; 1) thuộc đồ thị. - Vẽ đường thẳng đi qua hai điểm (0; 2) và (-1; 1).
Đồ thị hàm số y=x+2 đi qua hai điểm (0;2) và (-1;1).
4. Ứng Dụng của Hàm Số Bậc Nhất
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Mô tả mối quan hệ giữa hai đại lượng tỉ lệ: Ví dụ, quãng đường đi được của một vật chuyển động đều theo thời gian có thể được mô tả bằng hàm số bậc nhất.
- Giải các bài toán liên quan đến lãi suất: Lãi suất đơn có thể được tính bằng công thức là một hàm số bậc nhất.
- Phân tích dữ liệu: Trong thống kê, hàm số bậc nhất có thể được sử dụng để mô hình hóa mối quan hệ giữa các biến số.
Kết Luận
Hiểu rõ “hàm số bậc nhất có dạng” y = ax + b là bước quan trọng để nắm vững các kiến thức liên quan. Bài viết đã cung cấp đầy đủ lý thuyết, các dạng bài tập thường gặp và phương pháp giải, giúp học sinh tự tin hơn khi đối mặt với các bài toán về hàm số bậc nhất. Việc luyện tập thường xuyên và áp dụng kiến thức vào thực tế sẽ giúp củng cố và mở rộng hiểu biết về chủ đề này.