Hệ tọa độ Descartes là một công cụ toán học mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực từ thiết kế đồ họa đến khoa học máy tính. Vậy, Trục Tung Là X Hay Y? Để hiểu rõ hơn về hệ tọa độ Descartes và vai trò của từng trục, hãy cùng tìm hiểu chi tiết trong bài viết này.
Hệ Tọa Độ Descartes Là Gì? Lịch Sử Hình Thành
Hệ tọa độ Descartes, hay còn gọi là hệ tọa độ Cartesian, là một hệ thống xác định vị trí của một điểm trên mặt phẳng hoặc trong không gian bằng cách sử dụng các số tọa độ. Điểm đặc biệt của hệ tọa độ này là sử dụng các trục vuông góc, giao nhau tại gốc tọa độ O.
René Descartes, nhà toán học người Pháp, là người đã phát triển hệ tọa độ này vào thế kỷ 17. Phát minh của ông đã tạo ra một cuộc cách mạng trong toán học, kết nối đại số và hình học Euclide, và đặt nền móng cho hình học giải tích. Nhờ hệ tọa độ Descartes, chúng ta có thể biểu diễn các đường thẳng, đường cong và các hình hình học bằng các phương trình toán học. Ví dụ, phương trình x² + y² = r² biểu diễn một đường tròn có tâm tại gốc tọa độ và bán kính r.
Giải Thích Thuật Ngữ Hệ Tọa Độ Descartes: Trục Tung Là Gì?
Để hiểu rõ hơn về hệ tọa độ Descartes, chúng ta cần nắm vững các thuật ngữ cơ bản:
- Trục tọa độ: Là tập hợp các trục vuông góc với nhau, được sử dụng để xác định vị trí của một điểm.
- Trục hoành (trục x): Là đường thẳng nằm ngang trong hệ tọa độ hai chiều.
- Trục tung (trục y): Là đường thẳng thẳng đứng trong hệ tọa độ hai chiều, vuông góc với trục hoành.
- Mặt phẳng tọa độ (mặt phẳng Descartes): Là mặt phẳng được tạo bởi trục hoành và trục tung.
- Góc phần tư: Là bốn phần được chia bởi trục hoành và trục tung.
- Gốc tọa độ: Là điểm giao nhau giữa trục hoành và trục tung, ký hiệu là O, có tọa độ (0, 0).
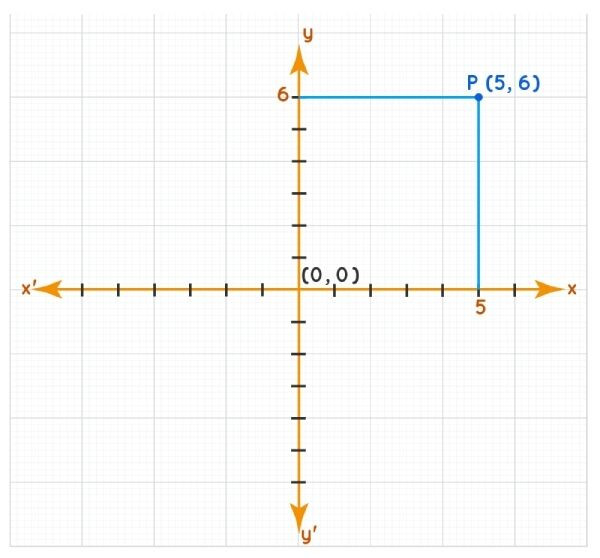
- Tọa độ của một điểm: Một điểm P bất kỳ trên mặt phẳng tọa độ được xác định bằng một cặp số (x, y), trong đó x là hoành độ (khoảng cách từ P đến trục tung) và y là tung độ (khoảng cách từ P đến trục hoành).
Các Hệ Trục Tọa Độ Descartes Thường Gặp
Có ba loại hệ tọa độ Descartes chính:
Hệ Tọa Độ Descartes Một Chiều
Đây là hệ tọa độ đơn giản nhất, chỉ bao gồm một trục duy nhất (hoặc trục hoành, hoặc trục tung) đi qua gốc tọa độ O. Mỗi điểm trên trục này được xác định bằng một số duy nhất, biểu thị khoảng cách từ điểm đó đến gốc tọa độ. Hệ tọa độ một chiều có thể được hình dung như một đường số.
Hệ Tọa Độ Trên Mặt Phẳng (Hai Chiều – 2D)
Hệ tọa độ Descartes hai chiều, hay còn gọi là mặt phẳng tọa độ, sử dụng hai trục vuông góc: trục hoành (x) và trục tung (y). Hai trục này chia mặt phẳng thành bốn góc phần tư.
Giá trị của các điểm trong các góc phần tư được xác định như sau:
- Góc phần tư thứ nhất: (x, y) (x dương, y dương)
- Góc phần tư thứ hai: (-x, y) (x âm, y dương)
- Góc phần tư thứ ba: (-x, -y) (x âm, y âm)
- Góc phần tư thứ tư: (x, -y) (x dương, y âm)
Hệ Tọa Độ Trong Không Gian (Ba Chiều – 3D)
Hệ tọa độ Descartes ba chiều mở rộng khái niệm của hệ tọa độ hai chiều bằng cách thêm một trục thứ ba, trục z (cao độ), vuông góc với cả trục x và trục y. Gốc tọa độ vẫn là điểm O (0, 0, 0). Hệ tọa độ này chia không gian thành tám phần.
Một điểm trong không gian được xác định bằng ba tọa độ (x, y, z), tương ứng với hoành độ, tung độ và cao độ.
Lưu Ý Quan Trọng Về Hệ Tọa Độ Descartes
Khi sử dụng hệ tọa độ Descartes, cần lưu ý những điểm sau:
- Gốc tọa độ có tọa độ (0, 0).
- Một điểm nằm trên trục x có tọa độ y = 0.
- Một điểm nằm trên trục y có tọa độ x = 0.
- Số lượng điểm trên một mặt phẳng tọa độ Descartes là vô số.
Hệ tọa độ Descartes là một công cụ nền tảng trong toán học và khoa học kỹ thuật. Việc hiểu rõ các khái niệm cơ bản, đặc biệt là việc trục tung là trục y, là rất quan trọng để áp dụng hiệu quả hệ tọa độ này trong các bài toán và ứng dụng thực tế.