Đường tròn ngoại tiếp tam giác là một khái niệm quan trọng trong hình học phẳng. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ về đường tròn ngoại tiếp tam giác, bao gồm định nghĩa, tính chất, cách xác định và các dạng bài tập thường gặp.
1. Định Nghĩa Đường Tròn Ngoại Tiếp Tam Giác
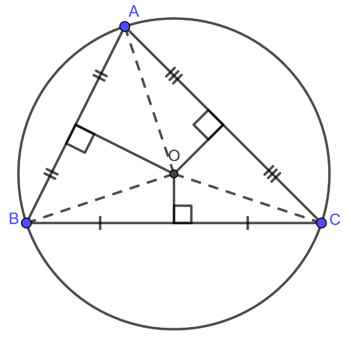
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó. Nói cách khác, tam giác nằm “nội tiếp” bên trong đường tròn. Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác. Đường tròn ngoại tiếp còn được gọi là đường tròn ngoại tiếp của tam giác.
Minh họa đường tròn ngoại tiếp tam giác ABC, tâm O là giao điểm các đường trung trực.
Nếu gọi O là tâm của đường tròn ngoại tiếp tam giác ABC, thì OA = OB = OC, và đều là bán kính R của đường tròn ngoại tiếp. Điều này có nghĩa là tâm đường tròn ngoại tiếp cách đều ba đỉnh của tam giác.
2. Tính Chất Quan Trọng của Đường Tròn Ngoại Tiếp Tam Giác
Đường tròn ngoại tiếp tam giác sở hữu những tính chất hữu ích, giúp giải quyết nhiều bài toán hình học:
- Duy nhất: Mỗi tam giác chỉ có một và duy nhất một đường tròn ngoại tiếp.
- Tâm đường tròn: Giao điểm của ba đường trung trực của tam giác là tâm của đường tròn ngoại tiếp.
- Tam giác vuông: Tâm đường tròn ngoại tiếp của tam giác vuông là trung điểm của cạnh huyền. Cạnh huyền đồng thời là đường kính của đường tròn.
- Tam giác đều: Tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp của tam giác đều trùng nhau.
3. Cách Xác Định và Vẽ Đường Tròn Ngoại Tiếp Tam Giác
3.1. Vẽ Đường Tròn Ngoại Tiếp
Để vẽ đường tròn ngoại tiếp một tam giác:
- Vẽ tam giác ABC.
- Dựng ba đường trung trực của ba cạnh tam giác.
- Xác định giao điểm I của ba đường trung trực. Điểm I là tâm của đường tròn ngoại tiếp.
- Vẽ đường tròn tâm I, bán kính IA (hoặc IB hoặc IC).
3.2. Xác Định Tâm Đường Tròn Ngoại Tiếp
Có hai cách phổ biến để xác định tâm của đường tròn ngoại tiếp tam giác:
-
Cách 1 (Sử dụng tọa độ):
- Gọi I(x; y) là tâm đường tròn ngoại tiếp tam giác ABC.
- Sử dụng tính chất IA = IB = IC = R (bán kính).
- Giải hệ phương trình: IA² = IB² và IA² = IC² để tìm tọa độ (x; y) của tâm I.
-
Cách 2 (Sử dụng phương trình đường trung trực):
- Viết phương trình hai đường trung trực của hai cạnh tam giác (ví dụ: cạnh AB và AC).
- Tìm giao điểm của hai đường trung trực đó. Giao điểm này chính là tâm của đường tròn ngoại tiếp.
Lưu ý: Đối với tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.
3.3. Phương Trình Đường Tròn Ngoại Tiếp Tam Giác
Để viết phương trình đường tròn ngoại tiếp tam giác, ta thực hiện các bước sau:
- Bước 1: Giả sử phương trình đường tròn có dạng: x² + y² + 2ax + 2by + c = 0. Thay tọa độ các đỉnh A, B, C của tam giác vào phương trình này.
- Bước 2: Giải hệ phương trình ba ẩn a, b, c để tìm ra các giá trị này.
- Bước 3: Thay các giá trị a, b, c vừa tìm được vào phương trình ban đầu, ta được phương trình đường tròn ngoại tiếp tam giác.
Mô tả phương trình đường tròn ngoại tiếp và cách tìm các hệ số.
3.4. Tính Bán Kính Đường Tròn Ngoại Tiếp
Bán kính đường tròn ngoại tiếp tam giác có thể được tính bằng công thức:
R = (abc) / (4S)
Trong đó:
- a, b, c là độ dài ba cạnh của tam giác.
- S là diện tích của tam giác.
Công thức này đặc biệt hữu dụng khi biết độ dài ba cạnh của tam giác. Diện tích tam giác có thể tính theo công thức Heron: S = √[p(p-a)(p-b)(p-c)], với p là nửa chu vi tam giác: p = (a+b+c)/2.
Công thức tính bán kính đường tròn ngoại tiếp tam giác thông qua độ dài các cạnh và diện tích tam giác.
4. Bài Tập Về Đường Tròn Ngoại Tiếp Tam Giác
Dưới đây là một số bài tập ví dụ về đường tròn ngoại tiếp tam giác:
Bài 1: Cho tam giác ABC với A(-1; 3), B(5; 1), C(-2; 3). Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Bài 2: Cho tam giác ABC với A(1; 3), B(-1; 1), C(2; 2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Bài 3: Tam giác ABC đều có cạnh bằng 8cm. Xác định bán kính và tâm của đường tròn ngoại tiếp tam giác ABC.
Bài 4: Tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 5: Cho tam giác MNP nhọn nội tiếp đường tròn (O; R). Ba đường cao MF, NE, PD cắt nhau tại H. Chứng minh tứ giác NDEP nội tiếp.
Hi vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về đường tròn ngoại tiếp tam giác. Hãy luyện tập giải các bài tập để nắm vững kiến thức và áp dụng thành thạo vào các bài toán hình học.