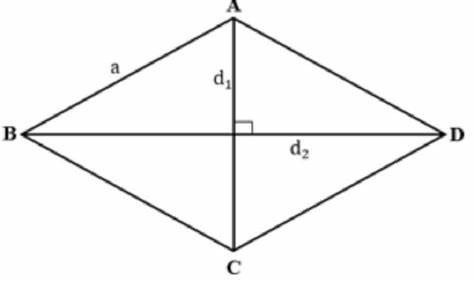
Hình thoi là một dạng tứ giác đặc biệt, thường xuất hiện trong các bài toán hình học và ứng dụng thực tế. Một trong những yếu tố quan trọng để hiểu và tính toán về hình thoi chính là đường Chéo Của Hình Thoi. Bài viết này sẽ cung cấp một cái nhìn toàn diện về đường chéo hình thoi, bao gồm định nghĩa, tính chất, công thức tính và các bài tập áp dụng.
Đường Chéo Hình Thoi Là Gì?
Đường chéo của hình thoi là đoạn thẳng nối hai đỉnh đối diện nhau của hình thoi đó. Mỗi hình thoi có hai đường chéo, và chúng đóng vai trò quan trọng trong việc xác định các đặc tính và tính toán liên quan đến hình thoi.
Các Tính Chất Quan Trọng Của Đường Chéo Hình Thoi
Hai đường chéo của hình thoi sở hữu những tính chất đặc biệt, phân biệt chúng với các tứ giác khác:
-
Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Điểm giao nhau của hai đường chéo chia mỗi đường thành hai đoạn bằng nhau.
-
Hai đường chéo vuông góc với nhau: Góc giữa hai đường chéo tại điểm giao nhau luôn là 90 độ.
-
Đường chéo là đường phân giác của các góc ở đỉnh: Mỗi đường chéo chia góc tại đỉnh mà nó đi qua thành hai góc bằng nhau.
-
Đường chéo chia hình thoi thành hai tam giác cân bằng nhau: Hai tam giác này có cạnh đáy là cạnh của hình thoi.
Công Thức Tính Đường Chéo Hình Thoi
Có nhiều cách để tính độ dài đường chéo của hình thoi, tùy thuộc vào thông tin đã biết:
1. Khi biết diện tích và đường chéo còn lại:
Từ công thức tính diện tích hình thoi: S = (d1 * d2) / 2
Trong đó:
Slà diện tích hình thoid1,d2là độ dài hai đường chéo
Ta có thể suy ra công thức tính độ dài một đường chéo khi biết diện tích và đường chéo còn lại:
d1 = (2 * S) / d2d2 = (2 * S) / d1
2. Khi biết cạnh và một góc:
Nếu biết độ dài cạnh a và một góc của hình thoi, ta có thể sử dụng các công thức lượng giác để tính độ dài đường chéo. Ví dụ, nếu góc đó là α, đường chéo ngắn hơn sẽ là 2*a*sin(α/2) và đường chéo dài hơn là 2*a*cos(α/2).
3. Sử dụng định lý Pythagoras:
Vì hai đường chéo vuông góc với nhau, chúng chia hình thoi thành bốn tam giác vuông bằng nhau. Nếu biết độ dài cạnh hình thoi a và một đường chéo d1, ta có thể tính đường chéo còn lại d2 bằng cách áp dụng định lý Pythagoras cho một trong các tam giác vuông:
(d1/2)^2 + (d2/2)^2 = a^2
Từ đó suy ra:
d2 = 2 * √(a^2 - (d1/2)^2)
Bài Tập Vận Dụng Về Đường Chéo Hình Thoi
Bài 1: Một hình thoi có diện tích là 720 cm², độ dài một đường chéo là 30 cm. Tính độ dài đường chéo còn lại.
Lời giải:
Áp dụng công thức: d2 = (2 * S) / d1 = (2 * 720) / 30 = 48 cm
Bài 2: Một hình thoi có cạnh dài 5 cm và một góc bằng 60 độ. Tính độ dài hai đường chéo của hình thoi.
Lời giải:
Đường chéo ngắn hơn: 2 * 5 * sin(60/2) = 2 * 5 * sin(30) = 5 cm
Đường chéo dài hơn: 2 * 5 * cos(60/2) = 2 * 5 * cos(30) = 5√3 cm
Bài 3: Cho hình thoi ABCD có cạnh AB = 13 cm và đường chéo AC = 10 cm. Tính độ dài đường chéo BD.
Lời giải:
Áp dụng định lý Pythagoras:
(AC/2)^2 + (BD/2)^2 = AB^2
(10/2)^2 + (BD/2)^2 = 13^2
25 + (BD/2)^2 = 169
(BD/2)^2 = 144
BD/2 = 12
BD = 24 cm
Bài 4: Hình thoi có hai đường chéo lần lượt là 8cm và 6cm. Tính chiều cao của hình thoi.
Lời giải:
Diện tích hình thoi là: (8 * 6) / 2 = 24 cm2
Độ dài cạnh của hình thoi là: √((8/2)^2 + (6/2)^2) = √(16+9) = 5cm
Chiều cao của hình thoi là: Diện tích/cạnh = 24/5 = 4.8 cm
Hiểu rõ về đường chéo của hình thoi giúp chúng ta giải quyết các bài toán hình học liên quan một cách hiệu quả. Nắm vững định nghĩa, tính chất và các công thức tính toán sẽ là nền tảng vững chắc cho việc học tập và ứng dụng kiến thức hình học vào thực tế.