Trong chương trình toán học, việc giải các bài toán liên quan đến hình chữ nhật là một phần quan trọng. Bài viết này sẽ tập trung vào một dạng toán điển hình: tính diện tích sân trường hình chữ nhật khi biết nửa chu vi và hiệu giữa chiều dài và chiều rộng.
Để giải quyết bài toán này, chúng ta cần áp dụng các kiến thức về chu vi, nửa chu vi và diện tích hình chữ nhật.
1. Tóm tắt kiến thức cần thiết
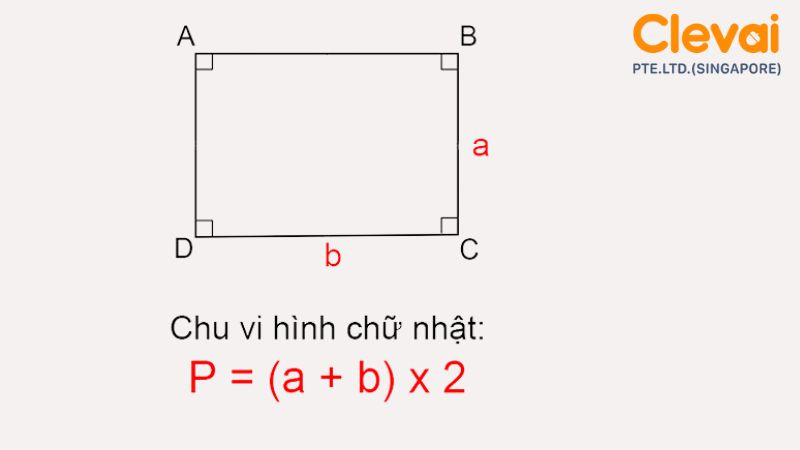
- Chu vi hình chữ nhật: P = 2 * (a + b), trong đó a là chiều dài, b là chiều rộng.
- Nửa chu vi hình chữ nhật: C = a + b
- Diện tích hình chữ nhật: S = a * b
2. Phân tích bài toán
Đề bài cho:
- Nửa chu vi sân trường hình chữ nhật: C = 26 m
- Chiều rộng kém chiều dài 8 m: a – b = 8 m
Yêu cầu: Tính diện tích sân trường hình chữ nhật: S = ?
3. Giải bài toán
Từ nửa chu vi, ta có phương trình: a + b = 26 (1)
Từ hiệu giữa chiều dài và chiều rộng, ta có phương trình: a – b = 8 (2)
Để giải hệ phương trình này, ta có thể sử dụng phương pháp cộng đại số:
Cộng (1) và (2), ta được:
(a + b) + (a – b) = 26 + 8
=> 2a = 34
=> a = 17 m
Thay a = 17 vào (1), ta được:
17 + b = 26
=> b = 9 m
Vậy, chiều dài sân trường là 17 m và chiều rộng sân trường là 9 m.
Diện tích sân trường là:
S = a b = 17 9 = 153 m2
Kết luận:
Diện tích sân trường hình chữ nhật là 153 m2.
4. Tổng kết và mở rộng
Bài toán “Sân Trường Hình Chữ Nhật Có Nửa Chu Vi Là 26 M Chiều Rộng Kém Chiều Dài 8 M Tính Diện Tích” là một ví dụ điển hình về ứng dụng kiến thức hình học vào giải quyết các vấn đề thực tế. Để giải tốt dạng bài này, học sinh cần nắm vững công thức tính chu vi, nửa chu vi, diện tích hình chữ nhật và kỹ năng giải hệ phương trình.
Ngoài ra, bài toán có thể được biến đổi bằng cách thay đổi các dữ kiện đã cho (ví dụ: cho chu vi và tỉ lệ giữa chiều dài và chiều rộng) để tạo ra các bài toán khác nhau, giúp học sinh rèn luyện tư duy và khả năng giải quyết vấn đề.