Trong hình học giải tích, việc xác định phương trình tiếp tuyến của đường tròn là một bài toán quan trọng và có nhiều ứng dụng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về Công Thức Tiếp Tuyến đường Tròn, từ lý thuyết cơ bản đến các dạng bài tập thường gặp và phương pháp giải quyết chúng.
1. Tổng Quan Về Đường Tròn
Đường tròn là tập hợp các điểm cách đều một điểm cố định (tâm) một khoảng không đổi (bán kính). Phương trình đường tròn có hai dạng chính:
-
Dạng chính tắc: Với tâm I(a; b) và bán kính R, phương trình là:
-
Dạng tổng quát: x² + y² – 2ax – 2by + c = 0, trong đó c = a² + b² – R². Điều kiện để phương trình này là phương trình đường tròn là a² + b² – c > 0. Khi đó, tâm đường tròn là I(a; b) và bán kính R = √(a² + b² – c).
2. Công Thức Tiếp Tuyến Đường Tròn
Tiếp tuyến của đường tròn là đường thẳng tiếp xúc với đường tròn tại một điểm duy nhất, gọi là tiếp điểm.
2.1. Tiếp Tuyến Tại Một Điểm Nằm Trên Đường Tròn
Cho đường tròn (C) có tâm I(a; b) và bán kính R. Gọi M₀(x₀; y₀) là một điểm nằm trên đường tròn (C). Khi đó, tiếp tuyến Δ của (C) tại M₀ có phương trình:
(x%20-%20x_0)%20+%20(y_0%20-%20b)(y%20-%20y_0)%20=%200)
Đây là dạng phương trình thu được từ việc sử dụng vectơ pháp tuyến IM₀ = (x₀ – a; y₀ – b) của tiếp tuyến Δ.
Cách nhớ nhanh (Tách đôi tọa độ):
-
Nếu (C): x² + y² – 2ax – 2by + c = 0 thì tiếp tuyến tại M₀(x₀; y₀) là: xx₀ + yy₀ – a(x + x₀) – b(y + y₀) + c = 0.
-
Nếu (C): (x – a)² + (y – b)² = R² thì tiếp tuyến tại M₀(x₀; y₀) là: (x – a)(x₀ – a) + (y – b)(y₀ – b) = R².
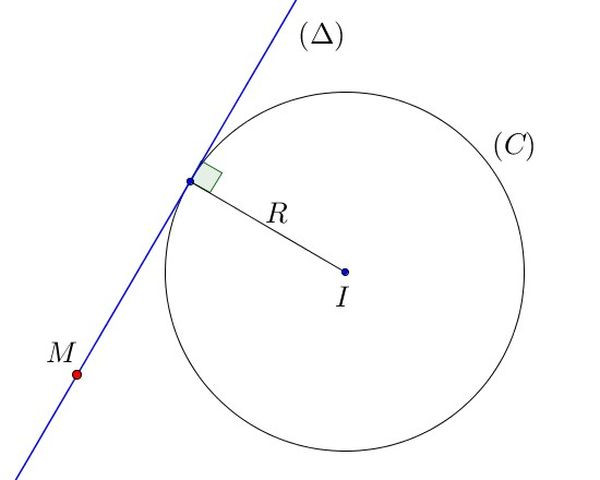Minh họa phương trình tiếp tuyến của đường tròn (C) tại điểm M0, với vectơ IM0 vuông góc với tiếp tuyến tại M0
2.2. Tiếp Tuyến Đi Qua Một Điểm Nằm Ngoài Đường Tròn
Khi điểm M₀(x₀; y₀) nằm ngoài đường tròn, ta thực hiện các bước sau:
- Viết phương trình đường thẳng Δ đi qua M₀(x₀; y₀) với hệ số góc k: y – y₀ = k(x – x₀) ⇔ kx – y – kx₀ + y₀ = 0.
- Sử dụng điều kiện tiếp xúc: Khoảng cách từ tâm I(a; b) của đường tròn đến đường thẳng Δ bằng bán kính R: d(I, Δ) = R.
- Giải phương trình d(I, Δ) = R để tìm giá trị của k. Thông thường, sẽ có hai giá trị của k, tương ứng với hai tiếp tuyến kẻ từ M₀ đến đường tròn.
- Thay các giá trị k tìm được vào phương trình đường thẳng Δ để được phương trình các tiếp tuyến.
2.3. Tiếp Tuyến Song Song Hoặc Vuông Góc Với Một Đường Thẳng Cho Trước
Cho đường thẳng d: Ax + By + C = 0.
-
Tiếp tuyến song song với d: Tiếp tuyến Δ có dạng Ax + By + m = 0 (m ≠ C). Sử dụng điều kiện d(I, Δ) = R để tìm m.
-
Tiếp tuyến vuông góc với d: Tiếp tuyến Δ có dạng Bx – Ay + m = 0. Sử dụng điều kiện d(I, Δ) = R để tìm m.
3. Các Dạng Bài Tập Về Tiếp Tuyến Đường Tròn
3.1. Viết Phương Trình Tiếp Tuyến Tại Một Điểm Thuộc Đường Tròn
Ví dụ: Cho đường tròn (C): (x – 1)² + (y + 2)² = 2. Viết phương trình tiếp tuyến của (C) tại A(3; -4).
Giải:
Đường tròn có tâm I(1; -2). Tiếp tuyến d tại A(3; -4) có phương trình:
(3 – 1)(x – 3) + (-4 + 2)(y + 4) = 0 ⇔ 2(x – 3) – 2(y + 4) = 0 ⇔ x – y – 7 = 0.
3.2. Viết Phương Trình Tiếp Tuyến Đi Qua Một Điểm Nằm Ngoài Đường Tròn
Ví dụ: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² – 4x – 4y + 4 = 0, biết tiếp tuyến đi qua B(4; 6).
Giải:
Đường tròn có tâm I(2; 2) và bán kính R = 2.
Gọi phương trình tiếp tuyến Δ: a(x – 4) + b(y – 6) = 0 ⇔ ax + by – 4a – 6b = 0.
Điều kiện tiếp xúc: d(I, Δ) = R ⇔ |2a + 2b – 4a – 6b| / √(a² + b²) = 2 ⇔ |-2a – 4b| = 2√(a² + b²) ⇔ |a + 2b| = √(a² + b²).
Bình phương hai vế: (a + 2b)² = a² + b² ⇔ a² + 4ab + 4b² = a² + b² ⇔ 4ab + 3b² = 0 ⇔ b(4a + 3b) = 0.
-
Nếu b = 0, chọn a = 1, ta được Δ: x – 4 = 0.
-
Nếu 4a = -3b, chọn a = 3 thì b = -4, ta được Δ: 3x – 4y + 12 = 0.
Vậy có hai tiếp tuyến thỏa mãn là x – 4 = 0 và 3x – 4y + 12 = 0.
3.3. Viết Phương Trình Tiếp Tuyến Song Song Với Một Đường Thẳng Cho Trước
Ví dụ: Cho đường tròn (C): (x – 3)² + (y + 1)² = 5. Viết phương trình tiếp tuyến của (C) song song với đường thẳng d: 2x + y + 7 = 0.
Giải:
Do tiếp tuyến song song với d: 2x + y + 7 = 0 nên phương trình tiếp tuyến có dạng Δ: 2x + y + m = 0 (m ≠ 7).
Đường tròn có tâm I(3; -1) và bán kính R = √5.
Điều kiện tiếp xúc: d(I, Δ) = R ⇔ |2.3 – 1 + m| / √5 = √5 ⇔ |5 + m| = 5 ⇔ 5 + m = 5 hoặc 5 + m = -5 ⇔ m = 0 hoặc m = -10.
Vậy Δ₁: 2x + y = 0, Δ₂: 2x + y – 10 = 0.
4. Bài Tập Luyện Tập
Câu 1: Cho đường tròn (C): (x – 3)² + (y – 1)² = 10. Phương trình tiếp tuyến của đường tròn (C) tại điểm A(4; 4) là:
A. x – 3y + 8 = 0. B. x + 3y – 16 = 0.
C. 2x – 3y + 5 = 0. D. x + 3y – 16 = 0.
Câu 2: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² – 4x – 4y + 4 = 0, biết tiếp tuyến đi qua điểm B(4; 6):
A. x – 4 = 0 hoặc 3x + 4y – 36 = 0 B. x – 4 = 0 hoặc y – 6 = 0.
C. y – 6 = 0 hoặc 3x + 4y – 36 = 0 D. x – 4 = 0 hoặc 3x – 4y + 12 = 0
(Còn nhiều câu hỏi khác…)
Kết Luận
Nắm vững công thức tiếp tuyến đường tròn và các phương pháp giải bài tập liên quan sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán hình học giải tích. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
