Lăng trụ đều là một dạng hình học không gian đặc biệt, thường gặp trong chương trình toán học phổ thông. Bài viết này sẽ đi sâu vào Tính Chất Lăng Trụ đều, cung cấp định nghĩa, các đặc điểm nhận dạng, công thức tính toán liên quan, và các bài tập minh họa có lời giải chi tiết.
Lăng Trụ Đều Là Gì?
Một hình lăng trụ được gọi là đều khi nó thỏa mãn hai điều kiện:
- Là lăng trụ đứng: Các cạnh bên vuông góc với mặt đáy.
- Đáy là đa giác đều: Tất cả các cạnh và góc của đa giác đáy bằng nhau.
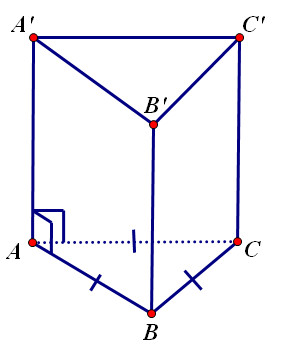
Ví dụ, lăng trụ tam giác đều có đáy là tam giác đều và các mặt bên là hình chữ nhật.
Tính Chất Quan Trọng Của Lăng Trụ Đều
Lăng trụ đều sở hữu những tính chất hình học đặc trưng, giúp việc tính toán và nhận dạng trở nên dễ dàng hơn:
- Hai mặt đáy là hai đa giác đều bằng nhau và song song.
- Các mặt bên là các hình chữ nhật bằng nhau và vuông góc với hai mặt đáy.
- Tất cả các cạnh bên đều bằng nhau và bằng chiều cao của lăng trụ.
- Các đường chéo của các mặt bên bằng nhau.
- Trong lăng trụ tứ giác đều (hình hộp chữ nhật), các đường chéo của lăng trụ bằng nhau.
Công Thức Tính Toán Liên Quan Đến Lăng Trụ Đều
Thể Tích
Thể tích của lăng trụ đều được tính bằng công thức:
V = S.h
Trong đó:
- V là thể tích của lăng trụ (đơn vị: m³, cm³…).
- S là diện tích đáy của lăng trụ (đơn vị: m², cm²…).
- h là chiều cao của lăng trụ, khoảng cách giữa hai mặt đáy (đơn vị: m, cm…).
Ví dụ, với lăng trụ tam giác đều có cạnh đáy là a và chiều cao là h, diện tích đáy là S = (a²√3)/4, do đó thể tích là V = (a²√3)/4 * h.
Diện Tích Xung Quanh và Diện Tích Toàn Phần
-
Diện tích xung quanh (Sxq): Là tổng diện tích của các mặt bên.
Sxq = P.h
Trong đó P là chu vi đáy và h là chiều cao của lăng trụ.
-
Diện tích toàn phần (Stp): Là tổng diện tích xung quanh và diện tích của hai đáy.
Stp = Sxq + 2Sđáy
Trong đó Sđáy là diện tích của một mặt đáy.
Bài Tập Vận Dụng Về Tính Chất Lăng Trụ Đều (Có Lời Giải Chi Tiết)
Bài 1: Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy AB = 4cm và chiều cao AA’ = 7cm. Tính thể tích của lăng trụ.
Giải:
Diện tích đáy ABC là: S = (4²√3)/4 = 4√3 cm²
Thể tích lăng trụ là: V = S.h = 4√3 * 7 = 28√3 cm³
Bài 2: Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy AB = 5cm và đường chéo AC’ = 5√3 cm. Tính chiều cao của lăng trụ và diện tích toàn phần.
Giải:
-
Tính chiều cao:
Áp dụng định lý Pythagoras trong tam giác vuông ACC’:
AC’^2 = AC^2 + CC’^2
(5√3)^2 = (5√2)^2 + CC’^2 (AC = 5√2 vì ABCD là hình vuông cạnh 5)
75 = 50 + CC’^2
CC’ = √25 = 5 cm (Vậy chiều cao của lăng trụ là 5cm)
-
Tính diện tích toàn phần:
Diện tích đáy: Sđáy = 5² = 25 cm²
Diện tích xung quanh: Sxq = P.h = (45)5 = 100 cm²
Diện tích toàn phần: Stp = Sxq + 2Sđáy = 100 + 2*25 = 150 cm²
Bài 3: Một lăng trụ lục giác đều có cạnh đáy bằng a và chiều cao bằng 2a. Tính thể tích của lăng trụ.
Giải:
Diện tích đáy của lăng trụ lục giác đều (gồm 6 tam giác đều):
Sđáy = 6 * (a²√3)/4 = (3a²√3)/2
Thể tích của lăng trụ:
V = Sđáy h = ((3a²√3)/2) 2a = 3a³√3
Ứng Dụng Thực Tế Của Lăng Trụ Đều
Hình lăng trụ đều xuất hiện nhiều trong thực tế, từ kiến trúc (các tòa nhà, cột trụ) đến các vật dụng hàng ngày (hộp đựng, lăng kính). Việc nắm vững tính chất lăng trụ đều giúp chúng ta dễ dàng tính toán kích thước, thể tích, và các thông số kỹ thuật cần thiết trong thiết kế và xây dựng.