Trong hình học, khái niệm “Tia đối Của Tia Ab” đóng vai trò quan trọng trong việc xác định vị trí tương đối của các điểm và đường thẳng. Bài viết này sẽ đi sâu vào định nghĩa, tính chất và các ứng dụng của tia đối, đồng thời làm rõ mối liên hệ giữa nó và các khái niệm hình học liên quan.
1. Định nghĩa tia đối của tia AB
Tia AB là một phần của đường thẳng đi qua hai điểm A và B, kéo dài vô tận về phía B. Tia đối của tia AB là tia có gốc tại A, nằm trên đường thẳng AB và kéo dài về phía ngược lại so với điểm B. Nói cách khác, nếu C là một điểm nằm trên tia đối của tia AB, thì A nằm giữa C và B.
2. Tính chất của tia đối
- Cùng nằm trên một đường thẳng: Tia AB và tia đối của nó cùng nằm trên một đường thẳng.
- Chung gốc: Cả hai tia đều có chung gốc là điểm A.
- Ngược hướng: Hai tia có hướng ngược nhau.
3. Ứng dụng của tia đối trong hình học
Khái niệm tia đối được sử dụng rộng rãi trong các bài toán hình học để:
- Xác định vị trí điểm: Xác định một điểm có nằm trên tia đối của một tia cho trước hay không.
- Chứng minh các định lý: Sử dụng tính chất của tia đối để chứng minh các định lý liên quan đến góc và đường thẳng.
- Giải các bài toán dựng hình: Dựng tia đối để tạo ra các hình có tính chất đặc biệt.
4. Mối liên hệ giữa tia đối và các khái niệm khác
- Đường thẳng: Tia AB và tia đối của nó hợp thành đường thẳng AB.
- Đoạn thẳng: Đoạn thẳng AB là một phần của tia AB.
- Góc: Tia đối của một cạnh của một góc có thể tạo thành góc bẹt hoặc góc tù.
Ví dụ minh họa:
Cho đường tròn tâm O, đường kính AB. Gọi M là một điểm bất kỳ trên đường tròn (M khác A và B). Vẽ tiếp tuyến tại A của đường tròn. Gọi C là một điểm trên tiếp tuyến sao cho A nằm giữa C và tiếp điểm. Khi đó, AC là tia đối của tia AB.
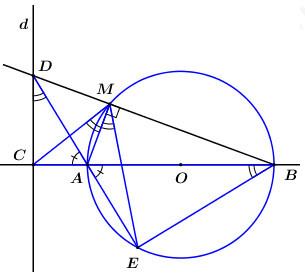Hình minh họa đường tròn và tiếp tuyến, AC là tia đối của AB
Alt: Hình vẽ minh họa đường tròn (O) đường kính AB, tiếp tuyến tại A có điểm C nằm trên tia đối của AB.
5. Bài tập vận dụng
Bài 1: Cho ba điểm A, B, C thẳng hàng, A nằm giữa B và C. Chứng minh rằng tia AB và tia AC là hai tia đối nhau.
Bài 2: Cho góc xOy khác góc bẹt. Vẽ tia Oz là tia phân giác của góc xOy. Vẽ tia Ot là tia đối của tia Oz. Chứng minh rằng góc xOt và góc yOt là hai góc kề bù.
Kết luận:
Hiểu rõ khái niệm “tia đối của tia AB” là nền tảng quan trọng để nắm vững các kiến thức hình học phức tạp hơn. Việc áp dụng linh hoạt các tính chất và ứng dụng của tia đối sẽ giúp giải quyết các bài toán hình học một cách hiệu quả và chính xác.
