Trong hình học không gian, việc tính Tỉ Lệ Thể Tích Khối Chóp là một kỹ năng quan trọng giúp giải quyết nhanh chóng và chính xác nhiều bài toán. Bài viết này tổng hợp các công thức và ví dụ minh họa điển hình về tỉ lệ thể tích khối chóp, bao gồm cả khối chóp tam giác và khối chóp có đáy là hình bình hành.
Tỉ Lệ Thể Tích Khối Chóp Tam Giác
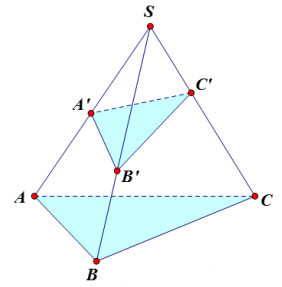
Cho khối chóp S.ABC và các điểm A’, B’, C’ lần lượt nằm trên các cạnh SA, SB, SC. Tỉ lệ thể tích của hai khối chóp S.A’B’C’ và S.ABC được tính theo công thức:
V(S.A’B’C’) / V(S.ABC) = (SA’/SA) (SB’/SB) (SC’/SC)
Hình ảnh minh họa khối chóp tam giác S.ABC với các điểm A’, B’, C’ trên các cạnh SA, SB, SC, thể hiện trực quan cho công thức tính tỉ lệ thể tích.
Công thức này đặc biệt hữu ích khi xác định thể tích một phần của khối chóp khi biết tỉ lệ các đoạn thẳng trên các cạnh bên.
Ví dụ, nếu A’ trùng với A, công thức trở thành:
V(S.AB’C’) / V(S.ABC) = (SB’/SB) * (SC’/SC)
Tỉ Lệ Thể Tích Khối Chóp Đáy Hình Bình Hành
Xét khối chóp S.ABCD có đáy ABCD là hình bình hành. Chọn các điểm A’, B’, C’, D’ lần lượt trên các cạnh SA, SB, SC, SD sao cho a + c = b + d, trong đó:
a = SA/SA’, b = SB/SB’, c = SC/SC’, d = SD/SD’
Khi đó, tỉ lệ thể tích giữa hai khối chóp S.A’B’C’D’ và S.ABCD là:
V(S.A’B’C’D’) / V(S.ABCD) = (a + b + c + d) / (4abcd)
Hình ảnh khối chóp S.ABCD với đáy là hình bình hành và các điểm A’, B’, C’, D’ trên các cạnh bên, minh họa cho công thức tính tỉ lệ thể tích trong trường hợp đáy là hình bình hành.
Công thức này giúp tính tỉ lệ thể tích một cách nhanh chóng khi biết các tỉ số đoạn thẳng trên các cạnh bên của khối chóp có đáy là hình bình hành.
Tỉ Lệ Thể Tích Hai Khối Chóp Chung Chiều Cao
Nếu hai khối chóp (H) và (H’) có diện tích đáy lần lượt là S và S’, và có chung chiều cao h, thì tỉ lệ thể tích của chúng là:
V(H’) / V(H) = S’ / S
Hình ảnh hai khối chóp có chung đỉnh và chiều cao, nhưng diện tích đáy khác nhau, thể hiện mối quan hệ tỉ lệ giữa thể tích và diện tích đáy.
Công thức này đặc biệt hữu dụng khi so sánh thể tích của các khối chóp có cùng chiều cao, giúp đơn giản hóa việc tính toán.
Tỉ Lệ Thể Tích Khối Đa Diện Đồng Dạng
Hai khối đa diện (H) và (H’) được gọi là đồng dạng với tỉ số k nếu tồn tại một phép đồng dạng F với tỉ số k biến (H) thành (H’). Khi đó, nếu AB là một cạnh của (H) và F(AB) = A’B’, thì A’B’ = kAB. Nếu V và V’ lần lượt là thể tích của (H) và (H’), ta có:
V’/V = k^3
Hình ảnh hai khối đa diện đồng dạng với nhau, thể hiện trực quan về tỉ lệ giữa các cạnh và thể tích của chúng.
Công thức này cho thấy thể tích của hai khối đa diện đồng dạng tỉ lệ với lập phương của tỉ số đồng dạng. Điều này rất quan trọng trong việc giải các bài toán liên quan đến sự thay đổi kích thước và thể tích của các hình khối.
Nắm vững các công thức và ví dụ trên sẽ giúp bạn giải quyết các bài toán về tỉ lệ thể tích khối chóp một cách hiệu quả và chính xác. Việc áp dụng linh hoạt các công thức này, kết hợp với kỹ năng hình dung không gian tốt, sẽ là chìa khóa để thành công trong các bài toán hình học không gian.