Bài toán tối ưu hóa chi phí sản xuất luôn là một vấn đề quan trọng đối với các doanh nghiệp. Trong nhiều trường hợp, Người Ta Dự định Dùng 2 Loại Nguyên Liệu khác nhau để tạo ra sản phẩm, và việc tìm ra tỉ lệ phối trộn tối ưu giữa hai loại nguyên liệu này có thể giúp giảm đáng kể chi phí. Bài viết này sẽ trình bày một ví dụ cụ thể về việc sử dụng phương pháp toán học để giải quyết bài toán này.
Giả sử một nhà máy cần sản xuất một sản phẩm chứa hai chất A và B. Người ta dự định dùng 2 loại nguyên liệu, loại I và loại II, để chiết xuất hai chất này. Mỗi tấn nguyên liệu loại I có giá 4 triệu đồng và chiết xuất được 20 kg chất A và 0,6 kg chất B. Mỗi tấn nguyên liệu loại II có giá 3 triệu đồng và chiết xuất được 10 kg chất A và 1,5 kg chất B.
Nhà máy cần ít nhất 140 kg chất A và 9 kg chất B. Ngoài ra, cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II. Mục tiêu là tìm số lượng nguyên liệu mỗi loại cần mua để chi phí là thấp nhất.
Gọi x là số tấn nguyên liệu loại I và y là số tấn nguyên liệu loại II cần dùng. Chúng ta có các ràng buộc sau:
- 0 ≤ x ≤ 10 (nguyên liệu loại I không vượt quá 10 tấn)
- 0 ≤ y ≤ 9 (nguyên liệu loại II không vượt quá 9 tấn)
- 20x + 10y ≥ 140 (đảm bảo đủ 140 kg chất A)
- 0.6x + 1.5y ≥ 9 (đảm bảo đủ 9 kg chất B)
Bài toán trở thành tìm giá trị nhỏ nhất của hàm chi phí F(x, y) = 4x + 3y, với (x, y) thỏa mãn các ràng buộc trên.
Để giải bài toán này, ta có thể sử dụng phương pháp đồ thị. Đầu tiên, vẽ miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ. Miền nghiệm này là một tứ giác ABCD, với các đỉnh là giao điểm của các đường thẳng biểu diễn các ràng buộc.
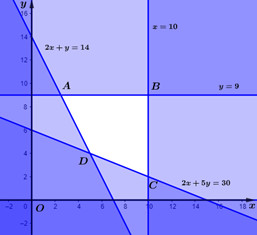Miền nghiệm bài toán tối ưu chi phí nguyên liệu
Sau khi xác định được miền nghiệm, ta tính giá trị của hàm chi phí F(x, y) tại các đỉnh của tứ giác ABCD. Đỉnh nào cho giá trị nhỏ nhất sẽ là nghiệm của bài toán.
Trong ví dụ này, các đỉnh của tứ giác là A(2.5; 9), B(10; 9), C(10; 2), và D(5; 4). Tính giá trị của F(x, y) tại các điểm này:
- F(A) = 4(2.5) + 3(9) = 37
- F(B) = 4(10) + 3(9) = 67
- F(C) = 4(10) + 3(2) = 46
- F(D) = 4(5) + 3(4) = 32
Ta thấy rằng F(D) là nhỏ nhất. Vậy, để chi phí mua nguyên liệu là ít nhất, người ta dự định dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II. Chi phí tối thiểu là 32 triệu đồng.
Bài toán này minh họa cách người ta dự định dùng 2 loại nguyên liệu và tối ưu hóa chi phí sản xuất bằng cách sử dụng các công cụ toán học. Việc phân tích kỹ lưỡng các ràng buộc và áp dụng các phương pháp tối ưu hóa có thể giúp doanh nghiệp tiết kiệm đáng kể chi phí và nâng cao hiệu quả sản xuất.
