Hình Chóp đáy Hình Thang Vuông là một dạng hình học không gian thường gặp trong chương trình toán phổ thông. Dưới đây là một bài toán điển hình và cách giải chi tiết, bao gồm cả hình vẽ minh họa và các công thức liên quan, giúp bạn nắm vững kiến thức về loại hình này.
Bài toán:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB = 2a, AD = DC = a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Lời giải:
a) Chứng minh các mặt phẳng vuông góc:
- Chứng minh (SAD) ⊥ (SDC):
Ta có AD ⊥ DC (do ABCD là hình thang vuông). Vì SA ⊥ (ABCD) nên SA ⊥ DC. Do đó, DC ⊥ (SAD). Vì DC nằm trong (SDC), suy ra (SAD) ⊥ (SDC).
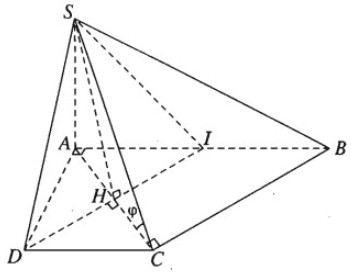Hình chóp S.ABCD với đáy là hình thang vuông ABCD và SA vuông góc với đáy, thể hiện mặt phẳng (SAD) vuông góc (SDC)
- Chứng minh (SAC) ⊥ (SCB):
Gọi I là trung điểm của AB. Khi đó AICD là hình vuông và IBCD là hình bình hành. Do DI // CB và DI ⊥ CA nên AC ⊥ CB. Vì vậy, CB ⊥ (SAC). Do CB nằm trong (SCB), suy ra (SAC) ⊥ (SCB).
b) Tính tanφ (góc giữa (SBC) và (ABCD)):
Góc giữa mặt phẳng (SBC) và (ABCD) là góc giữa đường cao kẻ từ S xuống BC và hình chiếu của nó trên (ABCD). Trong trường hợp này, hình chiếu của S trên (ABCD) là A.
Ta có:
- BC = √(BI² + IC²) = √(a² + a²) = a√2
- AB = 2a, AD = DC = a => góc ABC ≠ 90°. Do đó, ta cần tìm hình chiếu vuông góc của S xuống BC (gọi là H). Tính tan(góc SBH) = SA/AH. Mà AH ⊥ BC.
Kẻ AI vuông góc BC tại I. Vì SA vuông góc với (ABCD) nên BC vuông góc với (SAI). Vậy góc giữa (SBC) và (ABCD) là góc SAI.
Trong tam giác vuông ABC, ta có: 1/AI² = 1/AB² + 1/AC² = 1/(4a²) + 1/(2a²) = 3/(4a²) => AI = 2a/√3
Vậy tanφ = SA/AI = a / (2a/√3) = √3/2.
c) Xác định (α) và thiết diện của hình chóp với (α):
Mặt phẳng (α) chứa SD và vuông góc với (SAC). Gọi I là trung điểm AB. Ta có (SDI) vuông góc (SAC).
Do đó, (α) chính là mặt phẳng (SDI). Thiết diện của hình chóp S.ABCD với (α) là tam giác SDI. Tam giác SDI không đều mà cân tại S (SD = SI = a√2) và DI = a√2. H là tâm hình vuông AICD ta có SH ⊥ DI và SH = a√2/√2 = a
Tam giác SDI có diện tích: S = 1/2 SH DI = 1/2 a a√2 = (a²√2)/2
Kết luận:
Trên đây là một ví dụ điển hình về bài toán hình chóp đáy hình thang vuông. Việc nắm vững các kiến thức về quan hệ vuông góc trong không gian, cách xác định góc giữa hai mặt phẳng và cách tìm thiết diện là rất quan trọng để giải quyết các bài toán tương tự. Hy vọng bài viết này sẽ giúp ích cho bạn trong quá trình học tập và ôn luyện.
