Trong giải tích toán học, điểm Cực đại của một hàm số là một khái niệm quan trọng, giúp chúng ta hiểu rõ hơn về sự biến thiên và đặc điểm của hàm số đó. Bài viết này sẽ đi sâu vào định nghĩa, cách xác định và ứng dụng của điểm cực đại, đặc biệt trong bối cảnh giải toán và các bài toán thực tế.
Cho hàm số y = f(x) có đồ thị như hình vẽ:
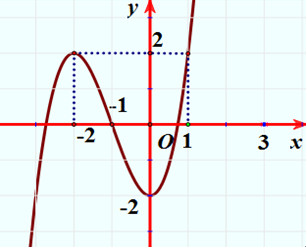Đồ thị hàm số minh họa điểm cực trị
Điểm cực đại của hàm số là điểm mà tại đó hàm số đạt giá trị lớn nhất trong một khoảng lân cận của điểm đó. Để hiểu rõ hơn, ta cần phân biệt giữa điểm cực đại và giá trị cực đại. Điểm cực đại là giá trị của biến số x, trong khi giá trị cực đại là giá trị của hàm số y = f(x) tại điểm cực đại đó.
Cách xác định điểm cực đại:
Có hai phương pháp chính để xác định điểm cực đại của hàm số:
-
Sử dụng đạo hàm bậc nhất:
- Tìm đạo hàm bậc nhất f'(x) của hàm số.
- Giải phương trình f'(x) = 0 để tìm các điểm tới hạn.
- Xét dấu của f'(x) xung quanh các điểm tới hạn. Nếu f'(x) đổi dấu từ dương sang âm khi x đi qua một điểm tới hạn, thì điểm đó là điểm cực đại.
-
Sử dụng đạo hàm bậc hai:
- Tìm đạo hàm bậc nhất f'(x) và đạo hàm bậc hai f”(x) của hàm số.
- Giải phương trình f'(x) = 0 để tìm các điểm tới hạn.
- Tính giá trị của f”(x) tại các điểm tới hạn. Nếu f”(x) < 0 tại một điểm tới hạn, thì điểm đó là điểm cực đại.
Ví dụ, xét bảng biến thiên của một hàm số:
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực tiểu tại x = 0. Đây là một ví dụ điển hình về cách xác định điểm cực trị dựa trên sự biến thiên của hàm số.
Ứng dụng của điểm cực đại:
Điểm cực đại có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau:
- Tối ưu hóa: Trong các bài toán tối ưu hóa, việc tìm điểm cực đại (hoặc cực tiểu) giúp xác định giá trị lớn nhất (hoặc nhỏ nhất) của một hàm số, từ đó tìm ra giải pháp tối ưu cho bài toán. Ví dụ, trong kinh tế, doanh nghiệp có thể sử dụng điểm cực đại để tối đa hóa lợi nhuận.
- Vật lý: Trong vật lý, điểm cực đại có thể được sử dụng để xác định vị trí mà một vật thể đạt độ cao lớn nhất trong quá trình chuyển động, hoặc để tìm ra cường độ lớn nhất của một trường điện từ.
- Kỹ thuật: Trong kỹ thuật, điểm cực đại có thể được sử dụng để thiết kế các cấu trúc có độ bền cao nhất, hoặc để tối ưu hóa hiệu suất của một hệ thống.
Lưu ý:
- Không phải hàm số nào cũng có điểm cực đại.
- Một hàm số có thể có nhiều điểm cực đại.
- Điểm cực đại chỉ là giá trị lớn nhất trong một khoảng lân cận, không nhất thiết là giá trị lớn nhất trên toàn bộ miền xác định của hàm số.
Hiểu rõ về điểm cực đại là một yếu tố quan trọng để nắm vững kiến thức về hàm số và ứng dụng chúng trong nhiều lĩnh vực khác nhau. Việc luyện tập giải các bài tập liên quan đến điểm cực đại sẽ giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán.
