Trong chương trình hình học lớp 7, chứng minh ba điểm thẳng hàng là một dạng toán quan trọng. Bài viết này sẽ cung cấp hướng dẫn chi tiết các phương pháp chứng minh, giúp học sinh nắm vững kiến thức và tự tin giải quyết các bài tập.
Thế Nào Là Ba Điểm Thẳng Hàng?
Ba điểm được gọi là thẳng hàng nếu chúng cùng nằm trên một đường thẳng. Đây là một khái niệm cơ bản nhưng đóng vai trò then chốt trong nhiều bài toán hình học.
Các Phương Pháp Chứng Minh 3 Điểm Thẳng Hàng Hiệu Quả
Dưới đây là các phương pháp thường được sử dụng, kèm theo giải thích và ví dụ minh họa để các em dễ dàng áp dụng:
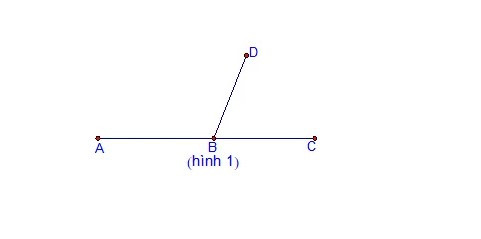
- Dựa vào tính chất góc bẹt: Chứng minh tổng hai góc kề nhau tạo thành một góc bẹt (180 độ). Nếu (widehat{ABD} + widehat{DBC} = 180^{circ}), thì A, B, C thẳng hàng.
- Tiên đề Ơ-Clit: Nếu hai đường thẳng cùng đi qua một điểm và song song với đường thẳng thứ ba, thì ba điểm đó thẳng hàng. Ví dụ, nếu AB // a và AC // a, thì A, B, C thẳng hàng.
- Tính chất hai đường thẳng vuông góc: Nếu hai đường thẳng cùng đi qua một điểm và vuông góc với đường thẳng thứ ba, thì ba điểm đó thẳng hàng. Ví dụ, nếu AB ⊥ a và AC ⊥ a, thì A, B, C thẳng hàng. Hoặc chứng minh 3 điểm cùng thuộc đường trung trực của 1 đoạn thẳng.
- Tính duy nhất của tia phân giác: Nếu OA và OB là hai tia phân giác của góc xOy, thì O, A, B thẳng hàng. Hoặc, nếu (widehat{xOA} = widehat{xOB}) và A, B cùng nằm trên nửa mặt phẳng bờ Ox, thì O, A, B thẳng hàng.
-
Tính chất đường trung trực: Nếu K là trung điểm của BD, và K’ là giao điểm của AC và BD, nếu K’ trùng với K thì A, K, C thẳng hàng.
-
Tính chất các đường đồng quy: Chứng minh 3 điểm thuộc các đường đồng quy của tam giác (trọng tâm, trực tâm, giao điểm ba đường phân giác, giao điểm ba đường trung trực). Ví dụ, chứng minh H là trọng tâm tam giác ABC và AM là trung tuyến, suy ra A, M, H thẳng hàng.
- Sử dụng vectơ: Chứng minh hai vectơ (overrightarrow{AB}) và (overrightarrow{AC}) (hoặc các cặp vectơ khác) cùng phương.
Bài Tập Vận Dụng
Để củng cố kiến thức, các em hãy thử sức với các bài tập sau:
- Bài 1: Cho tam giác ABC vuông tại A. Đường tròn đường kính AB cắt BC tại D. M là điểm bất kỳ trên AD. MH, MI vuông góc AB, AC tại H, I. HK vuông góc ID tại K. Chứng minh K, M, B thẳng hàng.
- Bài 2: Tam giác ABC vuông tại A. Vẽ đường tròn tâm B bán kính BA, đường tròn tâm C bán kính AC. Hai đường tròn giao nhau tại D. AM, AN là hai dây cung sao cho AN vuông góc AM và D nằm giữa M và N. Chứng minh M, D, N thẳng hàng.
- Bài 3: Nửa đường tròn (O; R) đường kính AB. C thuộc nửa đường tròn (C khác A và B). Gọi D là giao điểm của tiếp tuyến tại B với AC. Gọi E là giao điểm của BC và AD, F là giao điểm của BD và AC. I là trung điểm EF. Chứng minh IC là tiếp tuyến của (O).
- Bài 4: O là trung điểm AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ Ax và By sao cho (widehat{BAx} = widehat{ABy}). C, E thuộc Ax (E giữa A và C), D, F thuộc By (F giữa B và D) sao cho AC = BD, AE = BF. Chứng minh C, O, D thẳng hàng và E, O, F thẳng hàng.
- Bài 5: Tam giác ABC. Từ A vẽ xy // BC. M thuộc BC, vẽ các đường thẳng song song AB và AC, cắt xy tại D và E. Chứng minh AM, BD, CE đồng quy.
- Bài 6: Tam giác ABC. Trên tia đối AB lấy D sao cho AD = AB, trên tia đối AC lấy E sao cho AE = AC. M; N thuộc BC và ED sao cho CM = EN. Chứng minh M; A; N thẳng hàng.
Nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp các em tự tin chinh phục các bài toán chứng minh ba điểm thẳng hàng trong chương trình hình học lớp 7. Chúc các em học tốt!