Lăng trụ tam giác đều là một hình học không gian quan trọng, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ thông tin về định nghĩa, các tính chất đặc trưng của lăng trụ tam giác đều, cũng như các công thức liên quan.
Lăng Trụ Tam Giác Đều Là Gì?
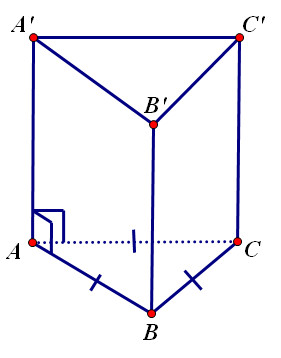
Lăng trụ tam giác đều là một loại lăng trụ đứng đặc biệt, có những đặc điểm sau:
- Hai đáy là hai tam giác đều bằng nhau.
- Các mặt bên là các hình chữ nhật bằng nhau và vuông góc với hai mặt đáy.
Tính Chất Quan Trọng Của Lăng Trụ Tam Giác Đều
Lăng trụ tam giác đều sở hữu những tính chất hình học đặc biệt, giúp chúng ta dễ dàng nhận biết và tính toán các thông số liên quan:
- Đáy là tam giác đều: Hai mặt đáy là hai tam giác đều có diện tích và kích thước hoàn toàn giống nhau. Điều này có nghĩa là tất cả các cạnh của tam giác đáy đều bằng nhau và các góc trong đều bằng 60 độ.
- Các cạnh đáy bằng nhau: Tất cả các cạnh của hai tam giác đáy đều có độ dài bằng nhau.
- Mặt bên là hình chữ nhật: Các mặt bên của lăng trụ tam giác đều là các hình chữ nhật có diện tích bằng nhau.
- Tính vuông góc: Các mặt bên của lăng trụ luôn vuông góc với cả hai mặt đáy. Đây là một tính chất quan trọng để xác định chiều cao của lăng trụ và tính toán thể tích.
Công Thức Tính Thể Tích và Diện Tích
Để giải các bài toán liên quan đến lăng trụ tam giác đều, chúng ta cần nắm vững các công thức tính thể tích và diện tích.
Thể Tích Lăng Trụ Tam Giác Đều
Thể tích (V) của lăng trụ tam giác đều được tính bằng công thức:
V = S.h
Trong đó:
- S là diện tích của mặt đáy (tam giác đều).
- h là chiều cao của lăng trụ (khoảng cách giữa hai mặt đáy).
Diện tích tam giác đều có cạnh a được tính bằng:
S = (a²√3)/4
Vậy, công thức tính thể tích lăng trụ tam giác đều trở thành:
V = ((a²√3)/4) * h
Diện Tích Xung Quanh
Diện tích xung quanh (Sxq) của lăng trụ tam giác đều là tổng diện tích của ba mặt bên hình chữ nhật. Nó được tính bằng công thức:
Sxq = P.h
Trong đó:
- P là chu vi của mặt đáy (tam giác đều).
- h là chiều cao của lăng trụ.
Chu vi của tam giác đều có cạnh a là:
P = 3a
Vậy, công thức tính diện tích xung quanh lăng trụ tam giác đều là:
Sxq = 3ah
Diện Tích Toàn Phần
Diện tích toàn phần (Stp) của lăng trụ tam giác đều là tổng của diện tích xung quanh và diện tích của hai mặt đáy:
Stp = Sxq + 2S
Trong đó:
- Sxq là diện tích xung quanh.
- S là diện tích của một mặt đáy (tam giác đều).
Vậy, công thức tính diện tích toàn phần lăng trụ tam giác đều là:
Stp = 3ah + 2 * ((a²√3)/4) = 3ah + (a²√3)/2
Bài Tập Vận Dụng
Bài tập: Một lăng trụ tam giác đều có cạnh đáy bằng 5cm và chiều cao bằng 10cm. Tính thể tích và diện tích toàn phần của lăng trụ.
Giải:
- Diện tích đáy: S = (5²√3)/4 = (25√3)/4 cm²
- Thể tích: V = S.h = ((25√3)/4) * 10 = (250√3)/4 cm³ ≈ 108.25 cm³
- Diện tích xung quanh: Sxq = 3510 = 150 cm²
- Diện tích toàn phần: Stp = 150 + 2 * ((25√3)/4) = 150 + (25√3)/2 cm² ≈ 171.65 cm²
Ứng Dụng Thực Tế
Lăng trụ tam giác đều không chỉ là một khái niệm hình học thuần túy, mà còn có nhiều ứng dụng trong thực tế, ví dụ:
- Kiến trúc và xây dựng: Được sử dụng trong thiết kế mái nhà, cột trụ, và các cấu trúc chịu lực.
- Thiết kế sản phẩm: Xuất hiện trong các chi tiết máy, hộp đựng, và các vật dụng gia đình.
- Quang học: Lăng kính tam giác được sử dụng để phân tách ánh sáng thành các thành phần màu sắc khác nhau.
Nắm vững các tính chất và công thức liên quan đến lăng trụ tam giác đều giúp chúng ta không chỉ giải quyết các bài toán hình học một cách hiệu quả, mà còn hiểu rõ hơn về cấu trúc và ứng dụng của nó trong thế giới xung quanh.