Bài toán Cho Tam Giác Abc Vuông Tại A Có các yếu tố và yêu cầu khác nhau, là một dạng bài tập hình học phổ biến trong chương trình Toán học phổ thông. Dưới đây, chúng ta sẽ cùng phân tích một ví dụ điển hình và mở rộng ra các ứng dụng liên quan.
Bài toán ví dụ:
Cho tam giác ABC vuông tại A, có CA = 4 và CB = 5. Gọi M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1.25. Tính độ dài đoạn thẳng MN.
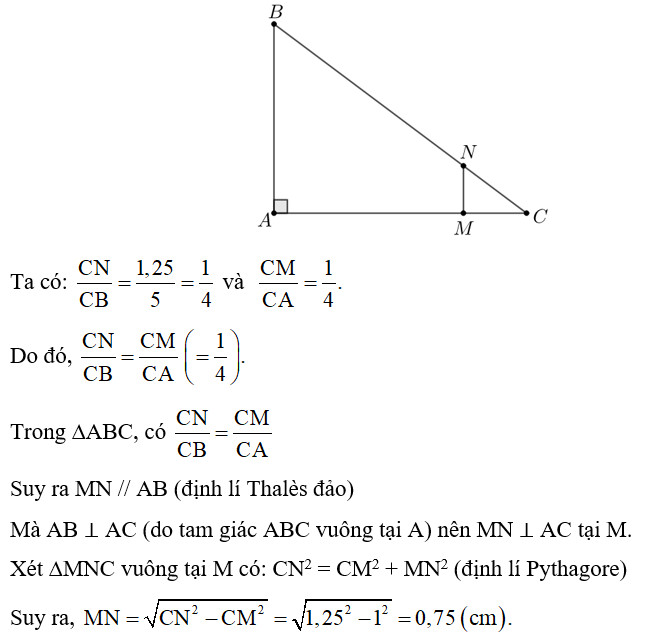Tam giác ABC vuông tại A với các điểm M, N trên cạnh CA, CB và các kích thước cho trước
Phân tích và giải bài toán:
Để giải bài toán này, chúng ta có thể sử dụng định lý Pytago để tìm độ dài cạnh AB của tam giác ABC vuông tại A. Sau đó, xét tỉ lệ các cạnh để chứng minh tam giác CMN đồng dạng với tam giác CBA, từ đó suy ra độ dài cạnh MN.
-
Tính AB:
- Áp dụng định lý Pytago cho tam giác ABC vuông tại A:
$AB^2 + AC^2 = BC^2$ - $AB^2 = BC^2 – AC^2 = 5^2 – 4^2 = 25 – 16 = 9$
- Vậy, $AB = sqrt{9} = 3$
- Áp dụng định lý Pytago cho tam giác ABC vuông tại A:
-
Xét tỉ lệ các cạnh:
- $frac{CM}{CA} = frac{1}{4}$
- $frac{CN}{CB} = frac{1.25}{5} = frac{1}{4}$
Vì $frac{CM}{CA} = frac{CN}{CB}$, suy ra tam giác CMN đồng dạng với tam giác CBA (theo trường hợp cạnh – góc – cạnh, với góc C chung).
-
Tính MN:
- Do tam giác CMN đồng dạng với tam giác CBA, ta có:
$frac{MN}{BA} = frac{CM}{CA}$ - $MN = BA frac{CM}{CA} = 3 frac{1}{4} = frac{3}{4} = 0.75$
- Do tam giác CMN đồng dạng với tam giác CBA, ta có:
Vậy, độ dài đoạn thẳng MN là 0.75 đơn vị độ dài.
Ứng dụng và mở rộng:
Bài toán cho tam giác ABC vuông tại A có nhiều ứng dụng trong thực tế và các bài toán hình học phức tạp hơn. Dưới đây là một số ví dụ:
- Ứng dụng trong xây dựng: Việc tính toán kích thước các cấu trúc dựa trên tam giác vuông, đảm bảo tính chính xác và an toàn.
- Ứng dụng trong trắc địa: Đo đạc địa hình, xác định khoảng cách và độ cao dựa trên các tam giác vuông.
- Ứng dụng trong thiết kế: Sử dụng tam giác vuông để tạo ra các hình dạng và cấu trúc độc đáo trong thiết kế đồ họa và kiến trúc.
Các bài toán liên quan:
Ngoài bài toán trên, dạng bài cho tam giác ABC vuông tại A có thể biến đổi với nhiều yếu tố khác nhau, ví dụ:
- Cho thêm đường cao AH, yêu cầu tính các đoạn thẳng liên quan đến đường cao.
- Cho thêm trung tuyến AM, yêu cầu chứng minh các tính chất liên quan đến trung tuyến.
- Kết hợp với các đường phân giác, đường trung trực để tạo ra các bài toán phức tạp hơn.
Việc nắm vững kiến thức về tam giác vuông, định lý Pytago và các định lý liên quan đến tam giác đồng dạng là chìa khóa để giải quyết các bài toán thuộc dạng cho tam giác ABC vuông tại A có một cách hiệu quả.
