Góc nội tiếp là một khái niệm quan trọng trong hình học phẳng, đặc biệt là khi nghiên cứu về đường tròn. Hiểu rõ về góc nội tiếp giúp giải quyết nhiều bài toán liên quan đến tính toán góc, chứng minh các tính chất hình học và ứng dụng trong thực tế.
Định Nghĩa Góc Nội Tiếp
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh của góc là hai dây cung của đường tròn đó. Cung nằm giữa hai cạnh của góc nội tiếp được gọi là cung bị chắn.
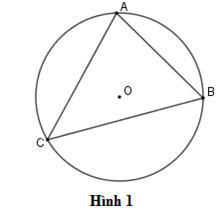Góc nội tiếp chắn cung AB
Trong hình trên, góc $widehat{ACB}$ là một góc nội tiếp chắn cung AB. Điểm C nằm trên đường tròn, và hai cạnh CA và CB là hai dây cung của đường tròn.
Định Lý Về Góc Nội Tiếp
Định lý quan trọng nhất liên quan đến góc nội tiếp là: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Ví dụ, nếu cung AB có số đo là 80 độ, thì góc nội tiếp $widehat{ACB}$ chắn cung AB sẽ có số đo là 40 độ.
Hệ Quả Của Định Lý Góc Nội Tiếp
Định lý về góc nội tiếp dẫn đến nhiều hệ quả quan trọng, được ứng dụng rộng rãi trong giải toán hình học:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau. Nếu hai góc nội tiếp cùng nằm trong một đường tròn và có số đo bằng nhau, thì hai cung bị chắn bởi hai góc đó cũng bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau. Nếu nhiều góc nội tiếp cùng chắn một cung, hoặc chắn các cung có độ dài bằng nhau, thì các góc đó bằng nhau.
- Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung. Góc ở tâm là góc có đỉnh là tâm của đường tròn. Nếu một góc nội tiếp và một góc ở tâm cùng chắn một cung, thì số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm.
- Góc nội tiếp chắn nửa đường tròn là góc vuông. Đây là một hệ quả quan trọng và thường được sử dụng để chứng minh tính vuông góc trong các bài toán hình học.
Các Dạng Toán Thường Gặp Về Góc Nội Tiếp
Các bài toán liên quan đến góc nội tiếp rất đa dạng, nhưng thường gặp nhất là các dạng sau:
-
Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau: Trong dạng toán này, ta thường sử dụng các hệ quả của định lý góc nội tiếp để suy ra các góc bằng nhau, từ đó chứng minh các tam giác đồng dạng hoặc các hệ thức liên quan.
-
Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích: Ta thường sử dụng hệ quả “Góc nội tiếp chắn nửa đường tròn là góc vuông” để chứng minh tính vuông góc. Ngoài ra, các hệ quả khác cũng có thể được sử dụng để suy ra các góc bằng nhau hoặc các mối quan hệ giữa các đoạn thẳng, từ đó giải quyết bài toán.
Ví dụ, xét bài toán sau: Cho đường tròn (O) đường kính AB. Lấy điểm C trên đường tròn sao cho AC < BC. Gọi H là hình chiếu vuông góc của C trên AB. Chứng minh rằng $widehat{ACH} = widehat{BCH}$.
Giải:
- Vì C nằm trên đường tròn (O) và AB là đường kính nên $widehat{ACB} = 90^circ$ (góc nội tiếp chắn nửa đường tròn).
- Xét tam giác ABC vuông tại C, ta có CH là đường cao nên $widehat{ACH} + widehat{HCB} = 90^circ$.
- Mặt khác, xét tam giác vuông ACH, ta có $widehat{CAH} + widehat{ACH} = 90^circ$.
- Từ đó suy ra $widehat{ACH} = widehat{BCH}$ (cùng phụ với $widehat{CAH}$).
Ứng Dụng Của Góc Nội Tiếp
Góc nội tiếp không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong các lĩnh vực như kiến trúc, kỹ thuật và thiết kế. Việc hiểu rõ về góc nội tiếp giúp chúng ta giải quyết các bài toán liên quan đến đo đạc, thiết kế các công trình có tính thẩm mỹ cao và đảm bảo tính chính xác.
Ví dụ, trong thiết kế các công trình kiến trúc có dạng vòm, việc tính toán chính xác các góc nội tiếp là rất quan trọng để đảm bảo tính cân đối và vững chắc của công trình. Trong kỹ thuật, góc nội tiếp được sử dụng trong các thiết bị đo đạc và định vị, giúp xác định vị trí và khoảng cách một cách chính xác.
Tóm lại, góc nội tiếp là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Việc nắm vững định nghĩa, định lý và các hệ quả của góc nội tiếp sẽ giúp chúng ta giải quyết nhiều bài toán hình học một cách hiệu quả và ứng dụng vào thực tế một cách sáng tạo.
