Hình Chóp Tam Giác: Khái Niệm, Công Thức và Bài Tập Ứng Dụng

Hình Chóp Tam Giác là một hình học không gian quen thuộc, xuất hiện nhiều trong các bài toán hình học và ứng dụng thực tế. Bài viết này sẽ cung cấp kiến thức đầy đủ về hình chóp tam giác, đặc biệt là hình chóp tam giác đều, cùng các công thức tính toán và bài tập minh họa.

Khái Niệm Hình Chóp Tam Giác

Hình chóp tam giác là hình chóp có đáy là một tam giác. Các mặt bên của hình chóp là các tam giác có chung một đỉnh, gọi là đỉnh của hình chóp.

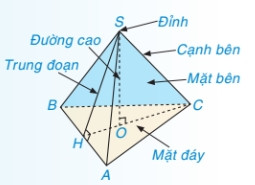Mô hình hình chóp tam giác với các thành phần chính được chú thích rõ ràng.

• Đỉnh: Điểm chung của các mặt bên (S trong hình vẽ).
• Đáy: Hình tam giác tạo thành mặt đáy (ví dụ: tam giác ABC).
• Mặt bên: Các mặt tam giác nối đỉnh với các cạnh của đáy (ví dụ: tam giác SAB, SBC, SCA).
• Cạnh bên: Các cạnh nối đỉnh với các đỉnh của đáy (ví dụ: SA, SB, SC).
• Đường cao: Đoạn thẳng vuông góc hạ từ đỉnh xuống mặt đáy.

Hình Chóp Tam Giác Đều

Hình chóp tam giác đều là hình chóp tam giác có đáy là một tam giác đều và các mặt bên là các tam giác cân bằng nhau, có chung đỉnh. Chân đường cao kẻ từ đỉnh tới mặt đáy trùng với trọng tâm của tam giác đáy.

Đặc điểm của hình chóp tam giác đều:

• Đáy là tam giác đều.
• Các mặt bên là các tam giác cân bằng nhau.
• Đường cao kẻ từ đỉnh vuông góc với trọng tâm của đáy.

Diện Tích Xung Quanh và Thể Tích Hình Chóp Tam Giác Đều

Diện Tích Xung Quanh

Diện tích xung quanh của hình chóp tam giác đều bằng tổng diện tích của các mặt bên. Vì các mặt bên là các tam giác cân bằng nhau, ta có công thức:

Trong đó:

• Sxq là diện tích xung quanh.
• p là nửa chu vi đáy (nửa chu vi của tam giác đều).
• d là trung đoạn của hình chóp (đường cao của một mặt bên).

Thể Tích

Thể tích của hình chóp tam giác đều được tính bằng công thức:

Trong đó:

• V là thể tích.
• S là diện tích đáy (diện tích của tam giác đều).
• h là chiều cao của hình chóp (khoảng cách từ đỉnh đến mặt đáy).

Bài Tập Về Hình Chóp Tam Giác Đều

Bài tập 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 6cm và chiều cao SH = 5cm. Tính thể tích của hình chóp.

Giải:

• Diện tích đáy (tam giác đều ABC): S = (cạnh² √3) / 4 = (6² √3) / 4 = 9√3 cm²
• Thể tích hình chóp S.ABC: V = (1/3) S h = (1/3) 9√3 5 = 15√3 cm³

Bài tập 2: Một đèn trang trí có dạng hình chóp tam giác đều, mỗi mặt là một tam giác đều cạnh 20cm. Tính diện tích giấy màu cần dùng để làm đèn (bỏ qua mép dán).

Giải:

• Tính trung đoạn (đường cao của mặt bên): Sử dụng định lý Pythagore trong tam giác vuông tạo bởi trung đoạn, nửa cạnh đáy và cạnh bên. Trung đoạn ≈ 17.32 cm.
• Nửa chu vi đáy: p = (20 + 20 + 20) / 2 = 30 cm
• Diện tích xung quanh (diện tích giấy màu cần dùng): Sxq = p trung đoạn = 30 17.32 = 519.6 cm²

Bài tập 3: Cho hình chóp tam giác đều P.QRS có cạnh đáy QR = 4cm và trung đoạn bằng 10cm. Tính diện tích xung quanh của hình chóp.

Giải:

• Nửa chu vi đáy: p = (4+4+4)/2 = 6 cm
• Diện tích xung quanh Sxq = p d = 6 10 = 60 cm²

Ứng Dụng Thực Tế

Hình chóp tam giác xuất hiện nhiều trong kiến trúc, xây dựng và thiết kế. Ví dụ, mái nhà, lều trại, kim tự tháp (dạng gần đúng) có thể được mô hình hóa bằng hình chóp tam giác. Việc nắm vững kiến thức về hình chóp tam giác giúp chúng ta hiểu rõ hơn về cấu trúc và tính toán các yếu tố liên quan trong thực tế.