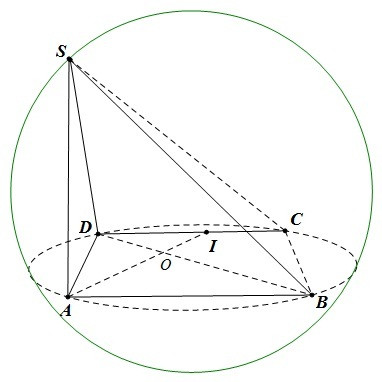
Mặt cầu ngoại tiếp tứ diện là mặt cầu đi qua tất cả các đỉnh của tứ diện đó. Việc xác định bán kính của mặt cầu này là một bài toán thường gặp trong chương trình hình học không gian lớp 12 và các kỳ thi quan trọng. Bài viết này sẽ cung cấp cho bạn các phương pháp hiệu quả và công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện, giúp bạn tự tin giải quyết các bài toán liên quan.
Các Phương Pháp Xác Định Tâm và Bán Kính Mặt Cầu Ngoại Tiếp Tứ Diện
Để tìm tâm và bán kính mặt cầu ngoại tiếp tứ diện ABCD, chúng ta có thể sử dụng một trong các phương pháp sau:
-
Sử dụng tính chất khoảng cách bằng nhau: Gọi I là tâm mặt cầu. Khi đó, ta có IA = IB = IC = ID = R (bán kính mặt cầu). Từ đó, ta có thể thiết lập hệ phương trình để tìm tọa độ tâm I và bán kính R.
-
Sử dụng phương trình mặt cầu tổng quát: Giả sử phương trình mặt cầu là $x^{2}+y^{2}+z^{2}+2ax+2by+2cz+d=0$. Vì mặt cầu đi qua 4 điểm A, B, C, D nên tọa độ của chúng phải thỏa mãn phương trình này. Ta sẽ có hệ 4 phương trình với 4 ẩn a, b, c, d. Giải hệ này, ta sẽ tìm được phương trình mặt cầu, từ đó suy ra tọa độ tâm và bán kính.
-
Sử dụng mặt phẳng trung trực: Viết phương trình các mặt phẳng trung trực của các đoạn thẳng AB, CD, BC. Giao điểm của ba mặt phẳng này chính là tâm của mặt cầu ngoại tiếp tứ diện ABCD.
Công Thức Tính Nhanh Bán Kính Mặt Cầu Ngoại Tiếp Tứ Diện
Để tính nhanh bán kính mặt cầu ngoại tiếp tứ diện, ta có thể áp dụng một số công thức đặc biệt tùy thuộc vào dạng của tứ diện. Dưới đây là một số trường hợp phổ biến:
Hình Chóp Đều
Trong trường hợp hình chóp đều, công thức tính bán kính mặt cầu ngoại tiếp trở nên đơn giản hơn.
Cho hình chóp đều có cạnh bên bằng a và chiều cao bằng h, bán kính R của mặt cầu ngoại tiếp được tính theo công thức:
$R = frac{a^{2}}{2h}$
Ví dụ: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng 3a. Để tính bán kính mặt cầu ngoại tiếp hình chóp này, ta thực hiện như sau:
- Xác định tâm O của hình vuông ABCD. SO sẽ vuông góc với mặt phẳng (ABCD).
- Tính AO: $AO = frac{AC}{2} = frac{asqrt{2}}{2}$
- Tính SO (chiều cao của hình chóp) bằng định lý Pythagoras trong tam giác vuông SAO: $SO = sqrt{SA^{2} – AO^{2}} = frac{asqrt{34}}{2}$
- Áp dụng công thức tính bán kính: $R = frac{SA^{2}}{2SO} = frac{9asqrt{34}}{34}$
Hình Chóp Có Cạnh Bên Vuông Góc Với Mặt Đáy
Nếu hình chóp có một cạnh bên vuông góc với mặt đáy, ta có công thức sau:
Gọi r là bán kính đường tròn ngoại tiếp đa giác đáy và h là chiều cao (cạnh bên vuông góc với đáy). Bán kính R của mặt cầu ngoại tiếp được tính bằng:
$R = sqrt{(frac{h}{2})^{2} + r^{2}}$
Ví dụ: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = 2a, OC = 2a. Tính bán kính R mặt cầu ngoại tiếp tứ diện này.
- Xác định chiều cao h = OA = a (vì OA vuông góc với mặt phẳng (OBC)).
- Tính BC: $BC = sqrt{OB^{2} + OC^{2}} = 2sqrt{2}a$
- Tính bán kính đường tròn ngoại tiếp tam giác OBC: $r = frac{BC}{2sin(angle BOC)} = frac{2sqrt{2}a}{2sin(90^{circ})} = asqrt{2}$
- Áp dụng công thức: $R = sqrt{(frac{a}{2})^{2} + (asqrt{2})^{2}} = frac{3a}{2}$
Hình Chóp Có Mặt Bên Vuông Góc Với Đáy
Trong trường hợp này, công thức tính bán kính mặt cầu ngoại tiếp phức tạp hơn một chút.
Gọi $R{b}$ và $R{d}$ lần lượt là bán kính đường tròn ngoại tiếp mặt bên và mặt đáy, GT là độ dài giao tuyến của mặt bên và mặt đáy. Khi đó:
$R = sqrt{R{b}^{2} + R{d}^{2} – frac{GT^{2}}{4}}$
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp.
- Xác định giao tuyến của (SAB) và (ABCD) là AB.
- Tính bán kính đường tròn ngoại tiếp đáy: $R_{d} = frac{AC}{2} = frac{asqrt{2}}{2}$
- Tính bán kính đường tròn ngoại tiếp mặt bên SAB (tam giác đều): $R_{b} = frac{a}{sqrt{3}} = frac{asqrt{3}}{3}$
- Áp dụng công thức: $R = sqrt{(frac{asqrt{3}}{3})^{2} + (frac{asqrt{2}}{2})^{2} – frac{a^{2}}{4}} = frac{asqrt{21}}{6}$
Bài Tập Vận Dụng
Để củng cố kiến thức, hãy cùng xem xét một số bài tập ví dụ:
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, BC = 4a, AB = 3a, SA = 12a và SA vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
Giải:
- Tính $R_{d} = frac{AC}{2} = frac{sqrt{AB^{2}+BC^{2}}}{2} = frac{5a}{2}$
- Áp dụng công thức: $R = sqrt{R_{d}^{2} + (frac{h}{2})^{2}} = sqrt{(frac{5a}{2})^{2} + (frac{12a}{2})^{2}} = frac{13a}{2}$
Bài 2: Cho hình chóp S.ABC có SA = SB = SC = a, $widehat{ASC}=widehat{ASB}=90^{circ}$. Tính diện tích S mặt cầu ngoại tiếp hình chóp.
Giải:
(Các bước giải chi tiết cần được bổ sung để hoàn thiện bài toán)
$S = 4pi R^{2} = …$
Bài 3: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB = a, $widehat{BAC}=120^{circ}$, cạnh bên SA = 2a và vuông góc với đáy (ABC). Tính bán kính R mặt cầu ngoại tiếp hình chóp.
Giải:
(Các bước giải chi tiết cần được bổ sung để hoàn thiện bài toán)
Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng (ABCD), SC = 2a. Tính bán kính mặt cầu ngoại tiếp hình chóp.
Giải:
(Các bước giải chi tiết cần được bổ sung để hoàn thiện bài toán)
Bài 5: Hình chóp S.ABC có đáy là tam giác vuông ABC vuông tại C, mặt phẳng (SAB) vuông góc với đáy, SA = SB = a và $widehat{ASB}=120^{circ}$. Tính bán kính mặt cầu ngoại tiếp hình chóp.
Giải:
(Các bước giải chi tiết cần được bổ sung để hoàn thiện bài toán)
Nắm vững các công thức và phương pháp trên, cùng với việc luyện tập thường xuyên, bạn sẽ dễ dàng chinh phục các bài toán về bán kính mặt cầu ngoại tiếp tứ diện trong các kỳ thi. Chúc bạn thành công!