Góc phần tư là một khái niệm quan trọng trong toán học, đặc biệt là khi làm việc với đường tròn lượng giác. Hiểu rõ cách Xác định Góc Phần Tư giúp bạn giải quyết các bài toán liên quan đến lượng giác một cách dễ dàng và chính xác.
1. Đường Tròn Lượng Giác và Góc Lượng Giác
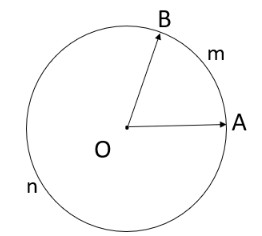
Đường tròn lượng giác là một đường tròn có bán kính bằng 1, tâm tại gốc tọa độ O(0,0) trong mặt phẳng Oxy. Chiều dương của đường tròn là chiều ngược chiều kim đồng hồ. Góc lượng giác là góc tạo bởi tia Ox và một tia khác xuất phát từ gốc O.
Alt: Hình ảnh đường tròn lượng giác với hai điểm A và B trên đường tròn, minh họa cung lượng giác AB.
2. Định Nghĩa Góc Phần Tư
Mặt phẳng tọa độ Oxy được chia thành bốn góc phần tư bởi hai trục Ox và Oy. Các góc phần tư được đánh số theo chiều ngược chiều kim đồng hồ, bắt đầu từ góc phần tư thứ nhất (I) ở góc trên bên phải.
- Góc phần tư thứ nhất (I): Nằm giữa 0° và 90° (hoặc 0 và π/2 radian).
- Góc phần tư thứ hai (II): Nằm giữa 90° và 180° (hoặc π/2 và π radian).
- Góc phần tư thứ ba (III): Nằm giữa 180° và 270° (hoặc π và 3π/2 radian).
- Góc phần tư thứ tư (IV): Nằm giữa 270° và 360° (hoặc 3π/2 và 2π radian).
3. Cách Xác Định Góc Phần Tư
Để xác định góc phần tư của một góc lượng giác, ta cần xác định điểm cuối của góc đó trên đường tròn lượng giác. Dựa vào vị trí của điểm cuối, ta có thể xác định góc đó thuộc góc phần tư nào.
Alt: Hình ảnh minh họa góc lượng giác trên đường tròn lượng giác, thể hiện mối quan hệ giữa góc và vị trí trên đường tròn.
4. Dấu của Các Giá Trị Lượng Giác trong Từng Góc Phần Tư
Dấu của các giá trị lượng giác (sin, cos, tan, cot) thay đổi tùy thuộc vào góc phần tư mà góc đó thuộc về. Điều này rất quan trọng khi giải các bài toán lượng giác.
- Góc phần tư I: sin > 0, cos > 0, tan > 0, cot > 0
- Góc phần tư II: sin > 0, cos < 0, tan < 0, cot < 0
- Góc phần tư III: sin < 0, cos < 0, tan > 0, cot > 0
- Góc phần tư IV: sin < 0, cos > 0, tan < 0, cot < 0
Alt: Đường tròn lượng giác biểu diễn trục giá trị của sin, cos, tan và cot, giúp xác định dấu của các hàm số lượng giác.
Alt: Bảng tổng hợp dấu của sin, cos, tan, cot trong từng góc phần tư, hỗ trợ việc xác định giá trị lượng giác.
5. Ứng Dụng của Việc Xác Định Góc Phần Tư
Việc xác định góc phần tư có nhiều ứng dụng trong giải toán lượng giác, bao gồm:
- Tìm giá trị lượng giác của các góc: Khi biết một giá trị lượng giác và góc thuộc góc phần tư nào, ta có thể xác định các giá trị lượng giác còn lại.
- Giải phương trình lượng giác: Việc xác định góc phần tư giúp ta tìm ra các nghiệm đúng của phương trình.
- Chứng minh các đẳng thức lượng giác: Xác định dấu của các giá trị lượng giác trong từng góc phần tư là một bước quan trọng trong việc chứng minh.
Alt: Đường tròn lượng giác minh họa các góc đặc biệt như 0, π/6, π/4, π/3, π/2 và mối liên hệ giữa chúng.
6. Ví Dụ Minh Họa
Ví dụ 1: Cho góc α = 210°. Hãy xác định góc phần tư mà góc này thuộc về và dấu của sinα, cosα.
- Giải: Góc 210° nằm giữa 180° và 270°, do đó nó thuộc góc phần tư thứ III.
- Trong góc phần tư thứ III, sinα < 0 và cosα < 0.
Ví dụ 2: Cho sinα > 0 và cosα < 0. Hãy xác định góc phần tư mà góc α thuộc về.
- Giải: sinα > 0 và cosα < 0 chỉ xảy ra ở góc phần tư thứ II.
Kết luận: Việc nắm vững cách xác định góc phần tư và dấu của các giá trị lượng giác trong từng góc phần tư là vô cùng quan trọng để giải quyết các bài toán lượng giác một cách hiệu quả. Hãy luyện tập thường xuyên để thành thạo kỹ năng này.