Đường chéo hình chữ nhật là một khái niệm hình học quan trọng, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Bài viết này sẽ cung cấp kiến thức đầy đủ về đường Chéo Hình Chữ Nhật, bao gồm định nghĩa, tính chất, công thức tính toán và các ví dụ minh họa, giúp bạn nắm vững kiến thức và áp dụng hiệu quả.
Đường Chéo Hình Chữ Nhật Là Gì?
Đường chéo của hình chữ nhật là đoạn thẳng nối hai đỉnh đối diện của hình đó. Mỗi hình chữ nhật có hai đường chéo và chúng có độ dài bằng nhau. Đường chéo đóng vai trò quan trọng trong việc xác định các đặc tính và tính toán liên quan đến hình chữ nhật.
Tính Chất Của Đường Chéo Hình Chữ Nhật
Đường chéo hình chữ nhật sở hữu những tính chất đặc biệt, giúp chúng ta giải quyết các bài toán liên quan một cách dễ dàng hơn:
- Bằng nhau: Hai đường chéo của hình chữ nhật luôn có độ dài bằng nhau.
- Cắt nhau tại trung điểm: Hai đường chéo cắt nhau tại trung điểm của mỗi đường, tạo thành bốn tam giác cân.
- Chia hình chữ nhật thành hai tam giác vuông: Mỗi đường chéo chia hình chữ nhật thành hai tam giác vuông có diện tích bằng nhau.
- Định lý Pytago: Đường chéo là cạnh huyền của một tam giác vuông, do đó có thể tính độ dài bằng định lý Pytago.
Công Thức Tính Đường Chéo Hình Chữ Nhật
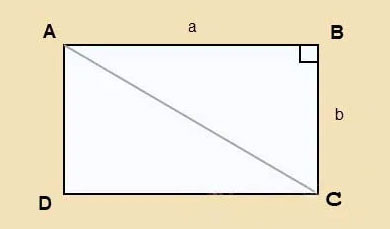
Để tính độ dài đường chéo hình chữ nhật, chúng ta sử dụng định lý Pytago. Giả sử hình chữ nhật ABCD có chiều dài là a và chiều rộng là b, đường chéo AC có thể được tính như sau:
Hình minh họa hình chữ nhật ABCD, chiều dài a, chiều rộng b và đường chéo AC, giúp người đọc hình dung rõ hơn về các yếu tố trong công thức tính đường chéo.
Áp dụng định lý Pytago cho tam giác vuông ABC, ta có:
AC² = AB² + BC² = a² + b²
Vậy, độ dài đường chéo AC của hình chữ nhật là:
AC = √(a² + b²)
Công thức này cho phép chúng ta tính độ dài đường chéo khi biết chiều dài và chiều rộng của hình chữ nhật.
Ví Dụ Minh Họa
Ví dụ 1: Tính độ dài đường chéo của một hình chữ nhật có chiều dài 8cm và chiều rộng 6cm.
Lời giải:
Áp dụng công thức tính đường chéo hình chữ nhật:
Đường chéo = √(8² + 6²) = √(64 + 36) = √100 = 10cm
Vậy, độ dài đường chéo của hình chữ nhật là 10cm.
Ví dụ 2: Một hình chữ nhật có chiều dài 12cm và đường chéo dài 13cm. Tính chiều rộng của hình chữ nhật.
Lời giải:
Gọi chiều rộng của hình chữ nhật là b. Áp dụng định lý Pytago:
13² = 12² + b²
169 = 144 + b²
b² = 169 – 144 = 25
b = √25 = 5cm
Vậy, chiều rộng của hình chữ nhật là 5cm.
Ứng Dụng Của Đường Chéo Hình Chữ Nhật
Đường chéo hình chữ nhật không chỉ là một khái niệm toán học đơn thuần, mà còn có nhiều ứng dụng thực tế trong cuộc sống và công việc:
- Thiết kế và xây dựng: Tính toán kích thước và độ vững chắc của các cấu trúc hình chữ nhật.
- Đo đạc: Xác định khoảng cách trực tiếp giữa hai điểm đối diện trong một khu vực hình chữ nhật.
- Cắt và ghép vật liệu: Tính toán đường cắt chéo để tối ưu hóa việc sử dụng vật liệu.
- Chứng minh hình học: Sử dụng các tính chất của đường chéo để chứng minh các bài toán liên quan đến hình chữ nhật.
Bài Tập Vận Dụng
Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:
- Một hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu chiều rộng là 5cm, tính độ dài đường chéo của hình chữ nhật.
- Đường chéo của một hình chữ nhật là 17cm và chiều rộng là 8cm. Tính chiều dài của hình chữ nhật.
- Một mảnh đất hình chữ nhật có chiều dài 20m và chiều rộng 15m. Tính độ dài đường chéo của mảnh đất.
Chứng Minh Tứ Giác Là Hình Chữ Nhật Thông Qua Đường Chéo
Tính chất đường chéo hình chữ nhật còn được ứng dụng để chứng minh một tứ giác là hình chữ nhật. Nếu một tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường, thì tứ giác đó là hình chữ nhật.
Hình ảnh minh họa các bước chứng minh tứ giác EFGH là hình chữ nhật dựa trên các tính chất đường trung bình và đường chéo.
Ví dụ: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, AD. Chứng minh rằng tứ giác EFGH là hình chữ nhật.
Lời giải:
- Chứng minh EFGH là hình bình hành (dựa vào tính chất đường trung bình).
- Chứng minh một góc của EFGH là góc vuông (dựa vào tính chất đường trung bình và đường chéo vuông góc của ABCD).
- Kết luận EFGH là hình chữ nhật (hình bình hành có một góc vuông).
Nắm vững kiến thức về đường chéo hình chữ nhật sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hy vọng bài viết này cung cấp cho bạn những thông tin hữu ích và cần thiết.