Vectơ Pháp Tuyến Là Gì?
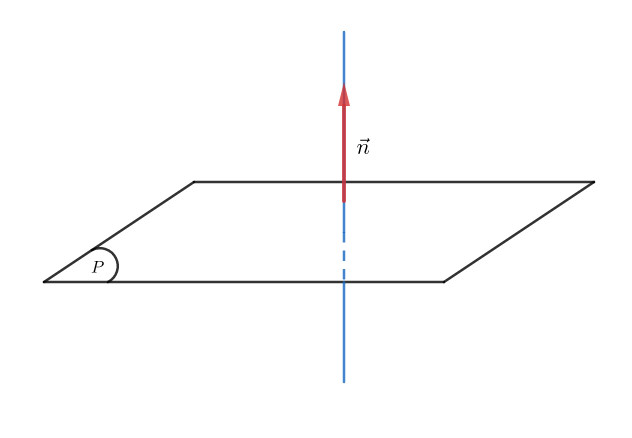
Trong không gian Oxyz, vectơ pháp tuyến của một mặt phẳng là một vectơ khác vectơ không và có phương vuông góc với mặt phẳng đó. Vectơ pháp tuyến đóng vai trò quan trọng trong việc xác định phương trình của mặt phẳng và giải quyết các bài toán liên quan đến vị trí tương đối, góc và khoảng cách.
Hình ảnh minh họa vectơ pháp tuyến, một vectơ vuông góc với mặt phẳng đang xét, giúp hình dung rõ hơn định nghĩa.
Phương Trình Mặt Phẳng và Vectơ Pháp Tuyến
Phương trình tổng quát của mặt phẳng trong không gian Oxyz có dạng:
Ax + By + Cz + D = 0
Trong đó, A, B, và C là các hệ số, và vectơ n = (A, B, C) chính là vectơ pháp tuyến của mặt phẳng. Điều này có nghĩa là, khi biết phương trình mặt phẳng, ta có thể dễ dàng xác định vectơ pháp tuyến của nó, và ngược lại.
Ứng Dụng của Vectơ Pháp Tuyến
Vectơ pháp tuyến có nhiều ứng dụng quan trọng trong hình học giải tích, bao gồm:
- Viết phương trình mặt phẳng: Khi biết một điểm thuộc mặt phẳng và vectơ pháp tuyến của nó, ta có thể viết được phương trình mặt phẳng.
- Xác định vị trí tương đối của hai mặt phẳng: Dựa vào tích vô hướng của hai vectơ pháp tuyến, ta có thể xác định hai mặt phẳng song song, vuông góc hoặc cắt nhau.
- Tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng bằng góc giữa hai vectơ pháp tuyến của chúng.
- Tính khoảng cách từ một điểm đến một mặt phẳng: Vectơ pháp tuyến được sử dụng trong công thức tính khoảng cách từ một điểm đến một mặt phẳng.
Các Dạng Bài Tập Thường Gặp
1. Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến:
Cho điểm M(x₀, y₀, z₀) và vectơ pháp tuyến n = (A, B, C). Phương trình mặt phẳng có dạng:
A(x - x₀) + B(y - y₀) + C(z - z₀) = 0
2. Viết phương trình mặt phẳng đi qua ba điểm không thẳng hàng:
Cho ba điểm A, B, và C. Vectơ pháp tuyến của mặt phẳng có thể được tìm bằng cách tính tích có hướng của hai vectơ AB và AC:
**n** = [**AB**, **AC**]
Sau đó, sử dụng một trong ba điểm A, B, hoặc C và vectơ pháp tuyến n để viết phương trình mặt phẳng.
3. Xác định vị trí tương đối của hai mặt phẳng:
Cho hai mặt phẳng (P₁) và (P₂) với các vectơ pháp tuyến lần lượt là n₁ = (A₁, B₁, C₁) và n₂ = (A₂, B₂, C₂).
- (P₁) song song với (P₂) khi và chỉ khi n₁ và n₂ cùng phương, tức là tồn tại số k sao cho n₁ = kn₂.
- (P₁) vuông góc với (P₂) khi và chỉ khi n₁.n₂ = 0, tức là A₁A₂ + B₁B₂ + C₁C₂ = 0.
Hình ảnh này minh họa cách xác định mối quan hệ song song, vuông góc, hay trùng nhau giữa hai mặt phẳng dựa trên các vectơ pháp tuyến tương ứng.
4. Tính góc giữa hai mặt phẳng:
Góc θ giữa hai mặt phẳng (P₁) và (P₂) được tính bằng công thức:
cos(θ) = |(**n₁**.**n₂**)| / (||**n₁**||.||**n₂**||)
5. Tính khoảng cách từ một điểm đến một mặt phẳng:
Khoảng cách từ điểm M(x₀, y₀, z₀) đến mặt phẳng (P): Ax + By + Cz + D = 0 được tính bằng công thức:
d(M, (P)) = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)
Công thức này cho phép tính khoảng cách ngắn nhất từ một điểm đến một mặt phẳng dựa vào vectơ pháp tuyến của mặt phẳng đó.
Ví Dụ Minh Họa
Ví dụ 1: Viết phương trình mặt phẳng (P) đi qua điểm M(1, 2, -1) và có vectơ pháp tuyến n = (2, -1, 3).
Giải:
Áp dụng công thức: A(x - x₀) + B(y - y₀) + C(z - z₀) = 0
Ta có: 2(x - 1) - 1(y - 2) + 3(z + 1) = 0
Rút gọn: 2x - y + 3z + 3 = 0
Vậy phương trình mặt phẳng (P) là: 2x - y + 3z + 3 = 0
Ví dụ 2: Cho hai mặt phẳng (P₁): x + 2y – z + 1 = 0 và (P₂): 2x + 4y – 2z + 3 = 0. Chứng minh (P₁) song song với (P₂).
Giải:
Vectơ pháp tuyến của (P₁) là n₁ = (1, 2, -1) và của (P₂) là n₂ = (2, 4, -2).
Ta thấy n₂ = 2n₁, suy ra n₁ và n₂ cùng phương.
Vậy (P₁) song song với (P₂).
Kết Luận
Hiểu rõ về vectơ pháp tuyến và các ứng dụng của nó là rất quan trọng để giải quyết các bài toán liên quan đến mặt phẳng trong không gian Oxyz. Nắm vững lý thuyết và luyện tập các dạng bài tập khác nhau sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán hình học giải tích.