Hình Chóp Đều Có Đáy Là Hình Gì?

Hình chóp đều là một dạng hình học không gian đặc biệt, và câu hỏi “Hình Chóp đều Có đáy Là Hình Gì?” là một câu hỏi quan trọng để hiểu rõ về loại hình này. Bài viết này sẽ giúp bạn nắm vững kiến thức về hình chóp đều, đặc biệt là hình chóp tam giác đều và hình chóp tứ giác đều.

1. Định Nghĩa Hình Chóp Đều

Hình chóp đều là hình chóp có những đặc điểm sau:

Đáy là một đa giác đều.
Hình chiếu của đỉnh chóp xuống mặt đáy trùng với tâm của đa giác đều đó.
Các cạnh bên của hình chóp đều bằng nhau.

2. Hình Chóp Tam Giác Đều

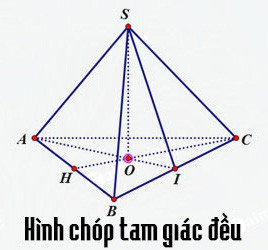
Hình chóp tam giác đều là hình chóp mà đáy của nó là một tam giác đều.

Tính chất của hình chóp tam giác đều:

Đáy là tam giác đều.
Các cạnh bên bằng nhau.
Các mặt bên là các tam giác cân bằng nhau.
Đường cao của hình chóp hạ từ đỉnh xuống đáy đi qua trọng tâm của tam giác đều (tâm đường tròn ngoại tiếp tam giác).
Các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
Các góc tạo bởi mặt bên và mặt đáy bằng nhau.

Diện tích và Thể tích hình chóp tam giác đều:

Diện tích xung quanh: (S_{xq} = p cdot d), trong đó p là nửa chu vi đáy, d là trung đoạn (chiều cao của mặt bên).
Diện tích toàn phần: (S{tp} = S{xq} + S), trong đó S là diện tích đáy.
Thể tích: (V = frac{1}{3} cdot S_{đáy} cdot h), trong đó h là chiều cao của hình chóp.

Cách vẽ hình chóp tam giác đều:

Vẽ tam giác đều ABC (có thể vẽ hình chiếu của tam giác đều).
Xác định tâm O của tam giác đều (giao điểm của ba đường trung tuyến).
Từ O, dựng đường thẳng vuông góc với mặt phẳng (ABC) (đường cao của hình chóp).
Lấy điểm S trên đường thẳng đó làm đỉnh của hình chóp.
Nối S với các đỉnh A, B, C để hoàn thành hình chóp S.ABC.

3. Hình Chóp Tứ Giác Đều

Hình chóp tứ giác đều là hình chóp có đáy là hình vuông.

Tính chất của hình chóp tứ giác đều:

Đáy là hình vuông.
Các cạnh bên bằng nhau.
Các mặt bên là các tam giác cân bằng nhau.
Đường cao của hình chóp hạ từ đỉnh xuống đáy đi qua giao điểm hai đường chéo của hình vuông (tâm hình vuông).
Các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
Các góc tạo bởi mặt bên và mặt đáy bằng nhau.

Diện tích và Thể tích hình chóp tứ giác đều:

Diện tích xung quanh: (S_{xq} = p cdot d), trong đó p là nửa chu vi đáy, d là trung đoạn (chiều cao của mặt bên).
Diện tích toàn phần: (S{tp} = S{xq} + S), trong đó S là diện tích đáy (diện tích hình vuông).
Thể tích: (V = frac{1}{3} cdot S_{đáy} cdot h), trong đó h là chiều cao của hình chóp.

4. Phân Biệt Hình Chóp Tam Giác Đều và Hình Chóp Tứ Giác Đều

Sự khác biệt chính giữa hình chóp tam giác đều và hình chóp tứ giác đều nằm ở hình dạng của đáy:

Hình chóp tam giác đều: Đáy là tam giác đều.
Hình chóp tứ giác đều: Đáy là hình vuông.

Ngoài ra, các tính chất và công thức tính toán cũng có sự khác biệt tương ứng với hình dạng của đáy.

5. Ứng Dụng và Bài Tập

Việc hiểu rõ về hình chóp đều, đặc biệt là hình chóp tam giác đều và hình chóp tứ giác đều, rất quan trọng trong hình học không gian và có nhiều ứng dụng thực tế trong kiến trúc, xây dựng và thiết kế. Hãy luyện tập giải các bài tập liên quan để nắm vững kiến thức và kỹ năng.