Một trong những khái niệm quan trọng trong giải tích hàm số là cực trị, đặc biệt là cực tiểu. Tuy nhiên, nhiều học sinh thường nhầm lẫn về việc cực tiểu của hàm số là giá trị x hay y. Bài viết này sẽ giải thích một cách chi tiết và dễ hiểu để bạn nắm vững kiến thức này.
Có rất nhiều em học sinh vẫn còn chưa nắm được chắc cũng như nắm được một cách khá mơ hồ về khái niệm cực trị là gì?. Hãy hiểu một cách đơn giản giá trị mà khiến hàm số đổi chiều khi biến thiên đó chính là cực trị của hàm số. Xét theo hình học, cực trị của hàm số biểu diễn khoảng cách lớn nhất từ điểm này sang điểm kia và ngược lại.
1. Định Nghĩa Cực Tiểu của Hàm Số
Để hiểu rõ “Cực Tiểu Của Hàm Số Là X Hay Y”, trước tiên cần nắm vững định nghĩa:
- Điểm cực tiểu (x₀): Là giá trị của biến số x tại đó hàm số đạt giá trị nhỏ nhất trong một lân cận nào đó của điểm đó.
- Giá trị cực tiểu (f(x₀)): Là giá trị của hàm số y tại điểm cực tiểu x₀, tức là y = f(x₀).
Như vậy, cực tiểu của hàm số là giá trị y (f(x₀)), còn x₀ là điểm mà tại đó hàm số đạt cực tiểu.
2. Phân Biệt Điểm Cực Tiểu và Giá Trị Cực Tiểu
Sai lầm phổ biến là lẫn lộn giữa điểm cực tiểu và giá trị cực tiểu. Hãy nhớ kỹ:
- Điểm cực tiểu (x): Thuộc trục hoành, cho biết vị trí mà hàm số đạt cực tiểu.
- Giá trị cực tiểu (y): Thuộc trục tung, cho biết độ lớn của giá trị nhỏ nhất mà hàm số đạt được tại điểm cực tiểu.
3. Điều Kiện Để Hàm Số Đạt Cực Tiểu
Để tìm điểm cực tiểu của hàm số, ta sử dụng đạo hàm. Có hai quy tắc chính:
3.1. Quy Tắc 1 (Sử dụng đạo hàm cấp nhất)
- Tính đạo hàm cấp nhất f'(x).
- Tìm các điểm xᵢ mà tại đó f'(xᵢ) = 0 hoặc f'(xᵢ) không tồn tại. Các điểm này gọi là điểm dừng.
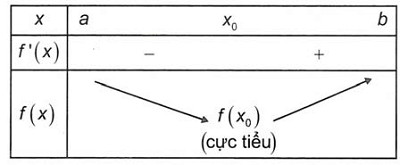
- Xét dấu của f'(x) trên các khoảng giữa các điểm dừng. Nếu f'(x) đổi dấu từ âm sang dương khi x đi qua x₀ thì x₀ là điểm cực tiểu.
Hình ảnh minh họa: Hàm số đạt cực tiểu khi đạo hàm f'(x) đổi dấu từ âm sang dương
3.2. Quy Tắc 2 (Sử dụng đạo hàm cấp hai)
-
Tính đạo hàm cấp nhất f'(x).
-
Giải phương trình f'(x) = 0 để tìm các nghiệm xᵢ.
-
Tính đạo hàm cấp hai f”(x).
-
Với mỗi nghiệm xᵢ, tính f”(xᵢ).
- Nếu f”(xᵢ) > 0 thì xᵢ là điểm cực tiểu.
- Nếu f”(xᵢ) < 0 thì xᵢ là điểm cực đại.
- Nếu f”(xᵢ) = 0 thì cần xét thêm (ví dụ, sử dụng quy tắc 1).
Hình ảnh minh họa: Hàm số đạt cực đại khi đạo hàm f'(x) đổi dấu từ dương sang âm
4. Ví Dụ Minh Họa
Xét hàm số f(x) = x² – 4x + 3.
- Tính f'(x) = 2x – 4.
- Giải f'(x) = 0 => x = 2.
- Tính f”(x) = 2. Vì f”(2) = 2 > 0 nên x = 2 là điểm cực tiểu.
Vậy, điểm cực tiểu của hàm số là x = 2, và giá trị cực tiểu là f(2) = 2² – 4*2 + 3 = -1.
Kết luận: Cực tiểu của hàm số f(x) = x² – 4x + 3 là y = -1.
5. Lưu Ý Quan Trọng
- Giá trị cực tiểu không nhất thiết là giá trị nhỏ nhất của hàm số trên toàn bộ tập xác định. Nó chỉ là giá trị nhỏ nhất trong một khoảng lân cận của điểm cực tiểu.
- Hàm số có thể có nhiều điểm cực tiểu.
6. Ứng Dụng Thực Tế
Hiểu rõ về cực trị của hàm số giúp giải quyết nhiều bài toán thực tế, ví dụ:
- Tìm giá thành sản xuất thấp nhất.
- Tìm lợi nhuận cao nhất.
- Tối ưu hóa các quy trình.
7. Các Dạng Bài Tập Thường Gặp
- Tìm điểm cực trị của hàm số.
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn cho trước.
- Biện luận số cực trị của hàm số theo tham số.
- Ứng dụng cực trị để giải các bài toán liên quan đến tiếp tuyến.
8. Tổng Kết
Bài viết này đã làm rõ khái niệm “cực tiểu của hàm số là x hay y”. Hy vọng bạn đã nắm vững kiến thức và có thể áp dụng để giải các bài tập liên quan một cách chính xác. Hãy luyện tập thêm để thành thạo và tự tin hơn với dạng toán này.