Vẽ Đường Tròn Nội Tiếp Tam Giác: Bí Quyết và Ứng Dụng

Đường tròn nội tiếp tam giác là một khái niệm quan trọng trong hình học, có nhiều ứng dụng thực tế và thường xuất hiện trong các bài toán. Bài viết này sẽ cung cấp kiến thức đầy đủ và sâu sắc về cách Vẽ đường Tròn Nội Tiếp Tam Giác, các tính chất liên quan và bài tập áp dụng.

Đường Tròn Nội Tiếp Tam Giác Là Gì?

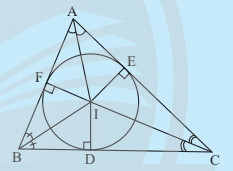
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác. Bán kính của đường tròn nội tiếp bằng khoảng cách từ tâm đến một cạnh bất kỳ của tam giác. Tam giác được gọi là tam giác ngoại tiếp đường tròn.

Hình ảnh minh họa đường tròn nội tiếp tam giác ABC, với tâm I là giao điểm của ba đường phân giác trong và bán kính r là khoảng cách từ I đến một cạnh bất kỳ.

Cách Vẽ Đường Tròn Nội Tiếp Tam Giác

Để vẽ đường tròn nội tiếp tam giác, ta thực hiện các bước sau:

Vẽ tam giác: Vẽ tam giác ABC bằng thước và compa.
Vẽ các đường phân giác: Dùng thước và compa vẽ hai đường phân giác trong của hai góc bất kỳ trong tam giác (ví dụ, góc A và góc B).
Xác định tâm đường tròn: Giao điểm của hai đường phân giác vừa vẽ là tâm I của đường tròn nội tiếp.
Vẽ đường tròn: Từ tâm I, vẽ một đường vuông góc xuống một cạnh bất kỳ của tam giác (ví dụ, cạnh BC). Độ dài đoạn vuông góc này là bán kính r của đường tròn nội tiếp.
Hoàn thành: Đặt compa vào tâm I, mở rộng bán kính bằng r và vẽ đường tròn. Đường tròn này chính là đường tròn nội tiếp tam giác ABC.

Hình ảnh minh họa các bước vẽ đường tròn nội tiếp tam giác ABC, bắt đầu bằng việc vẽ hai đường phân giác và xác định tâm đường tròn nội tiếp.

Tính Chất Quan Trọng Của Đường Tròn Nội Tiếp Tam Giác

Tâm đường tròn: Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.
Tiếp tuyến: Đường tròn nội tiếp tiếp xúc với cả ba cạnh của tam giác.
Bán kính: Bán kính của đường tròn nội tiếp có thể được tính bằng công thức:

r = S / p

trong đó:
- r là bán kính đường tròn nội tiếp
- S là diện tích của tam giác
- p là nửa chu vi của tam giác (p = (a + b + c) / 2, với a, b, c là độ dài các cạnh của tam giác)

Đường Tròn Nội Tiếp Trong Tam Giác Đặc Biệt

Tam giác đều

Trong tam giác đều, tâm của đường tròn nội tiếp trùng với trọng tâm, trực tâm và tâm đường tròn ngoại tiếp. Bán kính của đường tròn nội tiếp tam giác đều cạnh a là:

r = (a * căn bậc hai(3)) / 6

Tam giác vuông

Trong tam giác vuông, bán kính đường tròn nội tiếp có thể được tính bằng công thức:

r = (a + b - c) / 2

trong đó:

a và b là độ dài hai cạnh góc vuông
c là độ dài cạnh huyền

Bài Tập Vận Dụng Vẽ Đường Tròn Nội Tiếp Tam Giác

Bài 1: Cho tam giác ABC có AB = 6cm, BC = 8cm, CA = 10cm. Chứng minh tam giác ABC vuông và tính bán kính đường tròn nội tiếp tam giác đó.

Giải:

Chứng minh tam giác vuông: Ta thấy 6^2 + 8^2 = 36 + 64 = 100 = 10^2, vậy tam giác ABC vuông tại B theo định lý Pytago đảo.
Tính bán kính: Sử dụng công thức r = (a + b - c) / 2 = (6 + 8 - 10) / 2 = 2cm.

Bài 2: Cho tam giác đều ABC cạnh 4cm. Tính bán kính đường tròn nội tiếp tam giác đó.

Giải:

Sử dụng công thức r = (a * căn bậc hai(3)) / 6 = (4 * căn bậc hai(3)) / 6 = (2 * căn bậc hai(3)) / 3 cm.

Ứng Dụng Của Đường Tròn Nội Tiếp Tam Giác

Trong kiến trúc và xây dựng: Đường tròn nội tiếp được sử dụng để thiết kế các cấu trúc có tính thẩm mỹ và cân đối cao.
Trong thiết kế đồ họa: Đường tròn nội tiếp giúp tạo ra các hình ảnh hài hòa và cân đối.
Trong giải toán: Đường tròn nội tiếp là một công cụ hữu ích để giải các bài toán hình học phức tạp.

Kết Luận

Hiểu rõ cách vẽ đường tròn nội tiếp tam giác và các tính chất liên quan giúp chúng ta giải quyết nhiều bài toán hình học một cách dễ dàng và hiệu quả. Hy vọng bài viết này cung cấp cho bạn kiến thức đầy đủ và hữu ích về chủ đề này. Hãy luyện tập thường xuyên để nắm vững kỹ năng và áp dụng vào thực tế một cách sáng tạo.