1. Định Nghĩa và Vị Trí Cân Bằng của Con Lắc Đơn
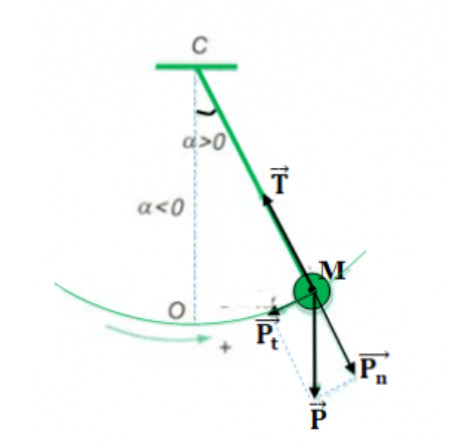
Một Con Lắc đơn là một hệ cơ học lý tưởng gồm một vật nhỏ (khối lượng m) treo vào một sợi dây không giãn, khối lượng không đáng kể, có chiều dài l. Con lắc đơn là một mô hình quan trọng trong vật lý, giúp chúng ta hiểu rõ hơn về dao động điều hòa.
Hình ảnh minh họa cấu tạo của một con lắc đơn, với khối lượng m gắn vào sợi dây có chiều dài l. Đây là mô hình vật lý cơ bản để nghiên cứu dao động.
Vị trí cân bằng của một con lắc đơn là vị trí mà sợi dây treo thẳng đứng. Khi kéo vật ra khỏi vị trí cân bằng một góc nhỏ rồi thả, vật sẽ dao động quanh vị trí cân bằng này.
Hình ảnh thể hiện vị trí cân bằng của một con lắc đơn, khi dây treo nằm theo phương thẳng đứng. Đây là điểm mà lực tác dụng lên vật cân bằng nhau.
2. Các Công Thức Quan Trọng về Dao Động của Con Lắc Đơn
2.1. Phương Trình Dao Động Điều Hòa
Trong điều kiện góc lệch nhỏ ($alpha$ < 10°), dao động của một con lắc đơn có thể được coi là dao động điều hòa. Phương trình dao động có dạng:
Phương trình dao động của con lắc đơn, biểu diễn mối quan hệ giữa li độ góc (α) và thời gian (t). Các thông số như biên độ góc (α₀) và tần số góc (ω) cũng được thể hiện.
Trong đó:
- s: Li độ dài (m, cm)
- S: Biên độ dài (m, cm)
- $alpha$: Li độ góc (rad)
- $alpha_0$: Biên độ góc (rad)
- $omega = sqrt{frac{g}{l}}$: Tần số góc (rad/s), với g là gia tốc trọng trường và l là chiều dài dây treo.
2.2. Chu Kỳ và Tần Số Dao Động
Chu kỳ (T) và tần số (f) của một con lắc đơn được tính theo công thức:
Chu kỳ:
Công thức tính chu kỳ dao động của con lắc đơn (T), phụ thuộc vào chiều dài dây treo (l) và gia tốc trọng trường (g).
Tần số:
Công thức tính tần số dao động của con lắc đơn (f), phụ thuộc vào chiều dài dây treo (l) và gia tốc trọng trường (g).
2.3. Vận Tốc và Lực Căng Dây
Vận tốc của vật nặng trong một con lắc đơn:
Công thức tính vận tốc của con lắc đơn tại một vị trí bất kỳ, phụ thuộc vào chiều dài dây treo (l), gia tốc trọng trường (g) và góc lệch.
Lực căng dây T:
- T = mg (3cosα – 2cosα0)
- Tmax = mg(3 – 2cosα0) (vật ở vị trí cân bằng)
- Tmin = mg(cosα0) (vật ở vị trí biên)
2.4. Cơ Năng, Động Năng, Thế Năng
- Cơ năng của một con lắc đơn (bỏ qua ma sát) được bảo toàn: W = $frac{1}{2}$mv2 + mgl(1 – cosα) = hằng số
- Động năng: Wđ = $frac{1}{2}$mv2 = $frac{1}{2}$ml2$dot{alpha}^{2}$
- Thế năng (mốc thế năng tại vị trí cân bằng): Wt = mgl(1 – cosα)
Từ đó suy ra: W = Wđ + Wt = hằng số
3. Ứng Dụng của Con Lắc Đơn
Một con lắc đơn có nhiều ứng dụng trong thực tế, đặc biệt trong việc xác định gia tốc trọng trường. Bằng cách đo chu kỳ dao động và chiều dài dây, ta có thể tính được gia tốc trọng trường tại một vị trí nhất định.
4. Bài Tập Vận Dụng về Con Lắc Đơn
Câu 1: Một con lắc đơn có chiều dài 1m, dao động điều hòa tại nơi có gia tốc trọng trường g = 9.8 m/s². Tính chu kỳ dao động của con lắc.
Giải:
Áp dụng công thức T = 2π$sqrt{frac{l}{g}}$ = 2π$sqrt{frac{1}{9.8}}$ ≈ 2.007 s
Câu 2: Một con lắc đơn có chiều dài 50 cm, khối lượng vật nặng là 200g. Kéo con lắc lệch khỏi vị trí cân bằng một góc 5° rồi thả nhẹ. Tính cơ năng của con lắc.
Giải:
Đổi 5° = 5 π / 180 ≈ 0.087 rad
Wtmax = mgl(1 – cosα0) = 0.2 9.8 0.5 (1 – cos(0.087)) ≈ 0.0037 J
Câu 3: Một con lắc đơn thực hiện 10 dao động toàn phần trong 20 giây. Tính chu kỳ và tần số dao động của con lắc.
Giải:
- Chu kỳ: T = 20/10 = 2 s
- Tần số: f = 1/T = 0.5 Hz
Hình ảnh bài tập ví dụ về con lắc đơn, minh họa cách áp dụng các công thức đã học để giải các bài toán liên quan đến chu kỳ, tần số và các đại lượng khác.
Nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp bạn hiểu rõ hơn về một con lắc đơn và ứng dụng của nó trong các bài toán vật lý.