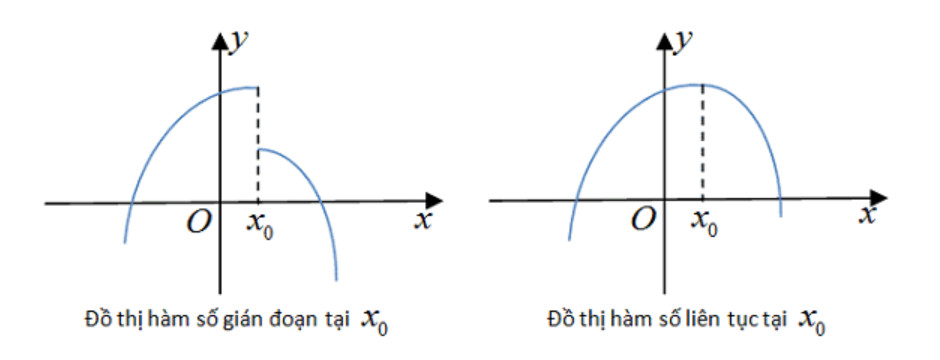Trong giải tích toán học, khái niệm hàm số liên tục đóng vai trò vô cùng quan trọng. Bài viết này sẽ tập trung vào “Hàm Số Liên Tục Tại 1 điểm”, cung cấp định nghĩa, các định lý liên quan, và các dạng bài tập thường gặp, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán.
Hàm Số Liên Tục Tại Một Điểm Là Gì?
Cho hàm số y = f(x) xác định trên khoảng (a; b) và $x_0 in (a; b)$. Hàm số y = f(x) được gọi là liên tục tại điểm $x_0$ nếu:
$$lim_{x to x_0} f(x) = f(x_0)$$
Nói cách khác, giới hạn của hàm số khi x tiến đến $x_0$ phải bằng giá trị của hàm số tại điểm đó. Nếu điều này không xảy ra, ta nói hàm số gián đoạn tại $x_0$, và $x_0$ được gọi là điểm gián đoạn của f(x).
Đồ thị hàm số liên tục, thể hiện sự liền mạch không có điểm gián đoạn, giúp hình dung trực quan tính liên tục của hàm số tại mọi điểm trên đồ thị.
Mở Rộng Về Tính Liên Tục
Nếu hai hàm số y = f(x) và y = g(x) cùng liên tục tại điểm $x_0$, thì các hàm số sau cũng liên tục tại $x_0$:
- y = f(x) + g(x)
- y = f(x) – g(x)
- y = f(x) * g(x)
Hàm số $y = frac{f(x)}{g(x)}$ liên tục tại $x_0$ nếu $g(x_0) neq 0$.
Hàm Số Liên Tục Trên Một Khoảng
Một hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm thuộc khoảng đó. Đồ thị của hàm số liên tục trên một khoảng là một đường liền nét, không bị đứt quãng.
Các hàm số như hàm căn thức, hàm phân thức, và hàm số lượng giác đều liên tục trên từng khoảng xác định của chúng.
Nếu hàm số y = f(x) liên tục trên khoảng (a; b) và thỏa mãn:
- $lim_{x to a^+} f(x) = f(a)$
- $lim_{x to b^-} f(x) = f(b)$
thì hàm số y = f(x) liên tục trên đoạn [a; b].
Hàm Số Liên Tục Trên R (Tập Số Thực)
Hàm số liên tục trên R là trường hợp đặc biệt của hàm số liên tục trên một khoảng. Một số hàm số đa thức, hàm lượng giác (y = sinx, y = cosx), hàm mũ và hàm phân thức có tập xác định R sẽ liên tục trên tập R mà không cần chứng minh.
Các Định Lý Cơ Bản Về Hàm Số Liên Tục
Để giải các bài tập liên quan đến hàm số liên tục, bạn cần nắm vững các định lý sau:
- Định lý 1: Hàm số đa thức liên tục trên R. Hàm phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng của tập xác định.
- Định lý 2: Nếu y = f(x) và y = g(x) liên tục tại $x_0$, thì y = f(x) + g(x), y = f(x) – g(x), và y = f(x) * g(x) cũng liên tục tại $x_0$. Ngoài ra, $y = frac{f(x)}{g(x)}$ liên tục tại $x_0$ nếu $g(x_0) neq 0$.
- Định lý 3 (Định lý Bolzano-Cauchy): Nếu hàm số y = f(x) liên tục trên [a; b] và f(a) * f(b) < 0, thì tồn tại ít nhất một số c thuộc (a; b) sao cho f(c) = 0. Điều này có nghĩa là phương trình f(x) = 0 có ít nhất một nghiệm trên khoảng (a; b).
Định lý 3 thường được sử dụng để chứng minh sự tồn tại nghiệm của phương trình trên một khoảng xác định.
Các Dạng Bài Tập Về Hàm Số Liên Tục và Ví Dụ
1. Xét Tính Liên Tục Của Hàm Số Tại Một Điểm
Các bước thực hiện:
-
Tính $f(x_0)$.
-
Tính $lim_{x to x0} f(x)$ (hoặc $lim{x to x0^+} f(x)$ và $lim{x to x_0^-} f(x)$).
-
So sánh $lim_{x to x_0} f(x)$ với $f(x_0)$.
- Nếu $lim_{x to x_0} f(x) = f(x0)$ (hoặc $lim{x to x0^+} f(x) = lim{x to x_0^-} f(x) = f(x_0)$), thì hàm số liên tục tại $x_0$.
- Nếu giới hạn không tồn tại hoặc $lim_{x to x_0} f(x) neq f(x_0)$, thì hàm số không liên tục tại $x_0$.
Ví dụ: Xét tính liên tục của hàm số sau tại x = 1:
$$f(x) = begin{cases} frac{2 – 7x + 5x^2}{x^2 – 3x + 2} & text{khi } x neq 1 -3 & text{khi } x = 1 end{cases}$$
Giải:
-
Hàm số xác định tại x = 1 và f(1) = -3.
-
Tính giới hạn:
$$lim{x to 1} f(x) = lim{x to 1} frac{2 – 7x + 5x^2}{x^2 – 3x + 2} = lim{x to 1} frac{(x – 1)(5x – 2)}{(x – 1)(x – 2)} = lim{x to 1} frac{5x – 2}{x – 2} = -3$$
-
Vì $lim_{x to 1} f(x) = f(1) = -3$, nên hàm số liên tục tại $x_0 = 1$.
Ví dụ minh họa hàm số gián đoạn tại một điểm, giới hạn trái và giới hạn phải không bằng nhau, cho thấy sự không liên tục.
2. Xét Tính Liên Tục Trên Một Khoảng, Đoạn Hoặc Tập Xác Định
Phương pháp: Sử dụng các định lý 1 và 2 để xét tính liên tục trên từng khoảng xác định. Sau đó, xét tính liên tục tại các điểm đặc biệt.
Ví dụ: Chứng minh hàm số sau liên tục trên khoảng (-7; +∞):
$$f(x) = begin{cases} x^2 – x + 4 & text{khi } x geq 2 frac{x – 2}{sqrt{x + 7} – 3} & text{khi } -7 x < 2 end{cases}$$
Giải: (Tham khảo giải chi tiết trong bài viết gốc)
Hình ảnh minh họa cách xét tính liên tục của hàm số trên một khoảng, tập trung vào việc kiểm tra các điểm chuyển tiếp và sử dụng định lý về giới hạn.
3. Tìm Điều Kiện Để Hàm Số Liên Tục Tại Một Điểm (Tìm m)
Các bước thực hiện:
- Tìm điểm xác định $x_0$.
- Tính $f(x_0)$ theo m.
- Tính $lim_{x to x_0} f(x)$.
- Sử dụng điều kiện liên tục: $lim_{x to x_0} f(x) = f(x_0)$ để tìm m.
Ví dụ: Tìm m để hàm số sau liên tục tại x = 1:
$$f(x) = begin{cases} frac{2 – 7x + 5x^2}{x^2 – 3x + 2} & text{khi } x neq 1 -3m & text{khi } x = 1 end{cases}$$
Giải:
-
Hàm số xác định tại x = 1 và f(1) = -3m.
-
Tính giới hạn:
$$lim{x to 1} f(x) = lim{x to 1} frac{2 – 7x + 5x^2}{x^2 – 3x + 2} = -3$$
-
Để hàm số liên tục tại x = 1, ta có: $lim_{x to 1} f(x) = f(1) Leftrightarrow -3 = -3m Leftrightarrow m = 1$
Hình ảnh minh họa bài toán tìm giá trị tham số ‘m’ để đảm bảo tính liên tục của hàm số tại một điểm cụ thể, thể hiện rõ các điều kiện cần thiết.
4. Tìm Điều Kiện Để Hàm Số Liên Tục Trên Một Khoảng, Đoạn Hoặc Tập Xác Định
Tương tự dạng 3, nhưng cần xét trên toàn bộ khoảng, đoạn hoặc tập xác định.
5. Ứng Dụng Tính Liên Tục Để Chứng Minh Phương Trình Có Nghiệm
Sử dụng định lý Bolzano-Cauchy: Nếu f(x) liên tục trên [a; b] và f(a) * f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm trên (a; b).
Ví dụ: Chứng minh rằng phương trình $3x^3 + 2x – 2 = 0$ có nghiệm trong (0; 1).
Giải:
- Hàm số $f(x) = 3x^3 + 2x – 2$ liên tục trên R (hàm đa thức).
- $f(0) = -2$ và $f(1) = 3$.
- $f(0) f(1) = -2 3 = -6 < 0$.
- Vậy, theo định lý Bolzano-Cauchy, phương trình $3x^3 + 2x – 2 = 0$ có ít nhất một nghiệm trong (0; 1).
6. Sử Dụng Tính Liên Tục Để Xét Dấu Hàm Số
Nếu hàm số y = f(x) liên tục và không triệt tiêu trên (a; b), thì nó giữ dấu không đổi trên khoảng này.
Bài Tập Luyện Tập
(Các bài tập và giải chi tiết trong bài viết gốc)
Bài 1: Xét tính liên tục của hàm số tại x = 0: …
Bài 2: Xét tính liên tục trên R của hàm số: …
Bài 3: Chứng minh phương trình … có nghiệm trong …
Bài 4: Tìm a để hàm số sau liên tục tại x = 2: …
Bài 5: Hàm số f(x) sau đây liên tục trên R khi nào? …
Kết Luận
Hiểu rõ về hàm số liên tục tại một điểm là nền tảng quan trọng để tiếp thu các kiến thức giải tích nâng cao. Nắm vững định nghĩa, các định lý và phương pháp giải các dạng bài tập sẽ giúp bạn tự tin chinh phục các bài toán liên quan. Chúc bạn học tốt!