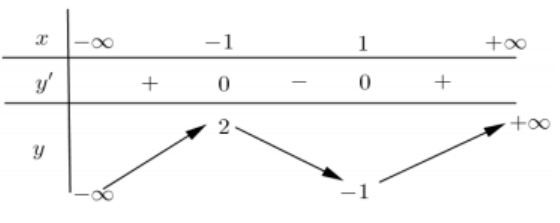
Câu hỏi: Cho hàm số y = f(x) có bảng biến thiên như sau:
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
Bảng biến thiên thể hiện sự biến thiên của hàm số f(x), giúp xác định khoảng nghịch biến dựa trên dấu của đạo hàm.
Giải thích chi tiết:
Để xác định hàm số nghịch biến trên khoảng nào, ta cần quan sát bảng biến thiên và tìm các khoảng mà tại đó f'(x) < 0 (đạo hàm âm) hoặc hàm số đi xuống.
Dựa vào bảng biến thiên trên, ta thấy hàm số nghịch biến trên các khoảng sau:
- (-2; 0)
- (2; +∞)
Trong các khoảng đáp án cho, nếu có một khoảng nào đó nằm trong (-2; 0) hoặc (2; +∞) thì đó là đáp án đúng. Ví dụ, khoảng (-2; -1) nằm trong khoảng (-2; 0) nên hàm số nghịch biến trên khoảng này.
Ví dụ minh họa khác:
Ví dụ 1: Cho hàm số y = f(x) có đồ thị như hình vẽ. Xác định khoảng nghịch biến của hàm số.
(Giả sử có hình ảnh đồ thị hàm số ở đây, đồ thị đi xuống từ x=a đến x=b)
Trong ví dụ này, ta quan sát đồ thị và thấy hàm số đi xuống (tức nghịch biến) từ x = a đến x = b. Vậy hàm số nghịch biến trên khoảng (a; b).
Ví dụ 2: Cho hàm số y = (x+1)/(x-2). Tìm khoảng nghịch biến của hàm số.
Để giải bài này, ta cần tìm đạo hàm của hàm số:
y’ = [(x-2) – (x+1)] / (x-2)^2 = -3 / (x-2)^2
Vì (x-2)^2 luôn dương (khi x ≠ 2) và -3 là số âm, nên y’ luôn âm với mọi x ≠ 2. Do đó, hàm số nghịch biến trên các khoảng (-∞; 2) và (2; +∞). Lưu ý rằng, ta không xét sự nghịch biến trên khoảng chứa điểm x = 2 vì hàm số không xác định tại điểm đó.
Lưu ý quan trọng:
- Điều kiện cần và đủ để hàm số nghịch biến:
- Điều kiện cần: Nếu hàm số y = f(x) nghịch biến trên khoảng (a; b) thì f'(x) ≤ 0 với mọi x thuộc (a; b).
- Điều kiện đủ: Nếu f'(x) < 0 với mọi x thuộc (a; b) thì hàm số y = f(x) nghịch biến trên khoảng (a; b).
- Xét các điểm không xác định: Cần loại bỏ các điểm mà tại đó hàm số không xác định khi xét khoảng nghịch biến. Ví dụ, hàm phân thức hữu tỷ không xác định tại điểm mà mẫu số bằng 0.
Các dạng bài tập thường gặp:
- Cho bảng biến thiên: Dựa vào dấu của f'(x) để xác định khoảng nghịch biến.
- Cho đồ thị hàm số: Quan sát đồ thị đi xuống để xác định khoảng nghịch biến.
- Cho biểu thức hàm số: Tính đạo hàm f'(x) và giải bất phương trình f'(x) < 0 để tìm khoảng nghịch biến.
- Bài toán liên quan đến tham số: Tìm giá trị của tham số để hàm số nghịch biến trên một khoảng cho trước.
Đồ thị hàm số bậc ba với đạo hàm f'(x) được sử dụng để xác định khoảng đồng biến, nghịch biến dựa vào dấu của f'(x).
Kết luận:
Việc xác định khoảng nghịch biến của hàm số là một kỹ năng quan trọng trong giải tích. Nắm vững lý thuyết, kết hợp với việc luyện tập các dạng bài tập khác nhau sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và chính xác. Chúc các bạn học tốt!