Hình thang là một dạng tứ giác đặc biệt với nhiều ứng dụng trong toán học và đời sống. Trong đó, hình thang vuông là một trường hợp thú vị. Bài viết này sẽ đi sâu vào Tính Chất đường Chéo Hình Thang Vuông, giúp bạn hiểu rõ và áp dụng hiệu quả.
1. Tổng Quan Về Hình Thang Vuông
Hình thang vuông là hình thang có ít nhất một góc vuông. Điều này có nghĩa là một trong hai cạnh bên của hình thang sẽ vuông góc với cả hai đáy.
Định nghĩa: Hình thang vuông là hình thang có một góc vuông (90°).
Tính chất cơ bản:
- Có ít nhất một cạnh bên vuông góc với hai đáy.
- Hai góc kề cạnh bên vuông góc là góc vuông.
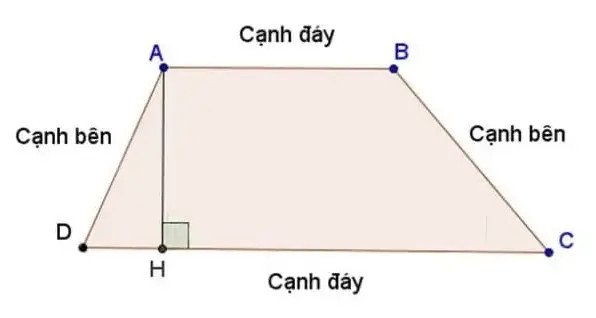Hình thang vuông với một góc vuông tại đỉnh A và D, cạnh AD vuông góc với hai đáy AB và DC.
2. Tính Chất Đường Chéo Hình Thang Vuông
Điểm đặc biệt khi xét đến tính chất đường chéo hình thang vuông là chúng không có tính chất đặc biệt nào so với hình thang thường.
Khẳng định: Trong hình thang vuông, hai đường chéo không bằng nhau và không chia đôi nhau.
Điều này khác biệt so với hình thang cân, nơi hai đường chéo bằng nhau. Sự khác biệt này xuất phát từ việc hình thang vuông không có tính đối xứng cao như hình thang cân.
3. So Sánh Đường Chéo Hình Thang Vuông với Hình Thang Khác
Để hiểu rõ hơn về tính chất đường chéo hình thang vuông, ta hãy so sánh nó với các loại hình thang khác:
- Hình thang thường: Hai đường chéo không bằng nhau và không chia đôi nhau. Tương tự như hình thang vuông.
- Hình thang cân: Hai đường chéo bằng nhau. Đây là điểm khác biệt lớn so với hình thang vuông.
| Loại hình thang | Tính chất đường chéo |
|---|---|
| Hình thang thường | Không bằng nhau, không chia đôi nhau |
| Hình thang vuông | Không bằng nhau, không chia đôi nhau |
| Hình thang cân | Bằng nhau |
4. Bài Tập Vận Dụng và Ứng Dụng Thực Tế
Mặc dù đường chéo hình thang vuông không có tính chất đặc biệt, việc hiểu rõ về chúng vẫn rất quan trọng khi giải các bài toán hình học. Dưới đây là một số ứng dụng và bài tập vận dụng:
- Tính diện tích: Để tính diện tích hình thang vuông, ta cần biết độ dài hai đáy và chiều cao (cạnh bên vuông góc). Đường chéo không trực tiếp tham gia vào công thức tính diện tích, nhưng có thể được sử dụng để tìm các thông số cần thiết khác.
- Chứng minh hình học: Trong các bài toán chứng minh, việc nhận biết hình thang vuông và tính chất của nó giúp ta suy luận và chứng minh các yếu tố khác của hình.
5. Kết Luận
Tính chất đường chéo hình thang vuông tuy đơn giản (không bằng nhau) nhưng lại là một phần quan trọng để phân biệt nó với các loại hình thang khác, đặc biệt là hình thang cân. Hiểu rõ điều này giúp ích rất nhiều trong quá trình học tập và ứng dụng hình học vào thực tế.
